Steve Awodey の Category Theory を読む シリーズトップ
- 8.3 The Yoneda lemma
- 8.4 Applications of the Yoneda lemma
- 8.5 Limits in categories of diagrams
- 8.6 Colimits in categories of diagrams
- 8.7 Exponentials in categories of diagrams
- 8.8 Topoi
- 参考書籍
8.3 The Yoneda lemma
書籍の lemma 8.2 の証明は contravariant 版の米田の埋め込みに関する証明ですが、covariant 版の米田の埋め込みに対しても同様の lemma が成立します。
つまり を 任意の
に対して
、任意の
に対して
で定義します。
このとき lemma 8.2 と同様に、任意の と任意の
に対して
が成立し、
は埋め込みになります。
証明自体は書籍にある lemma 8.2 の証明とほとんど同じなので省略します。理解の確認のためにこちらの証明を書籍を見ながらやってみるといいと思います。
8.4 Applications of the Yoneda lemma
、
、
に関しては transpose を取る対応なので、exponential の UMP より同型となります。
同型射として と
を取る。
このとき、任意の に対して
を示せばよい。つまり
を示せばよい。
\begin{align*}
& \pi_{X} \circ \pi_{X \times C} \circ \left< \left<\pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> \circ \left< \pi_{X} \circ \pi_{X \times C}, \left< \pi_{B}, \pi_{C} \circ \pi_{X \times C} \right> \right> \\
&= \pi_{X} \circ \left< \pi_{X} \circ \pi_{X \times C}, \left< \pi_{B}, \pi_{C} \circ \pi_{X \times C} \right> \right> \\
&= \pi_{X} \circ \pi_{X \times C}
\end{align*}
\begin{align*}
& \pi_{C} \circ \pi_{X \times C} \circ \left< \left<\pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> \circ \left< \pi_{X} \circ \pi_{X \times C}, \left< \pi_{B}, \pi_{C} \circ \pi_{X \times C} \right> \right> \\
&= \pi_{C} \circ \pi_{B \times C} \circ \left< \pi_{X} \circ \pi_{X \times C}, \left< \pi_{B}, \pi_{C} \circ \pi_{X \times C} \right> \right> \\
&= \pi_{C} \circ \pi_{X \times C}
\end{align*}
\begin{align*}
& \pi_{B} \circ \left< \left<\pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> \circ \left< \pi_{X} \circ \pi_{X \times C}, \left< \pi_{B}, \pi_{C} \circ \pi_{X \times C} \right> \right> \qquad \\
&= \pi_{B} \circ \pi_{B \times C} \circ \left< \pi_{X} \circ \pi_{X \times C}, \left< \pi_{B}, \pi_{C} \circ \pi_{X \times C} \right> \right> \\
&= \pi_{B}
\end{align*}
が成り立つので、product の UMP より が成り立つ。
任意の に対して
の証明も同様である。
次にそれぞれの同型射に関して、それが natural transformation であることを証明します。
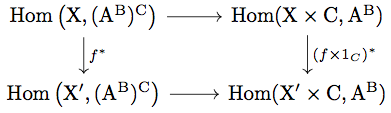
任意の と
に対して
\begin{align*}
(f \times 1_{C})^{\ast}(\overline{g}) &= \overline{g} \circ (f \times 1_{C}) \\
&= \epsilon \circ (g \times 1_{C}) \circ (f \times 1_{C}) \\
&= \epsilon \circ \left( (g \circ f) \times 1_{C} \right) \\
&= \overline{g \circ f} \\
&= \overline{f^{\ast}(g)}
\end{align*}
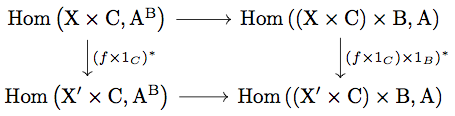
任意の と
に対して
\begin{align*}
\left( (f \times 1_{C}) \times 1_{B} \right)^{\ast}(\overline{g}) &= \overline{g} \circ \left( (f \times 1_{C}) \times 1_{B} \right) \\
&= \epsilon \circ (g \times 1_{B}) \circ \left( (f \times 1_{C}) \times 1_{B} \right) \\
&= \epsilon \circ \left( (g \circ (f \times 1_{C}) \times 1_{B} \right) \\
&= \overline{g \circ (f \times 1_{C})} \\
&= \overline{(f \times 1_{C})^{\ast}(g)}
\end{align*}
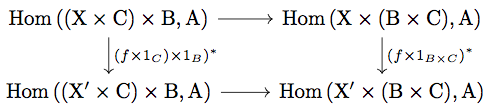
任意の と
に対して
\begin{align*}
\left( (f \times 1_{B \times C})^{\ast} \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right>^{\ast} \right)(g) &= g \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> \circ (f \times 1_{B \times C}) \\
&= g \circ \left( (f \times 1_{C}) \times 1_{B} \right) \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> \\
&= \left( \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right>^{\ast} \circ \left( (f \times 1_{C}) \times 1_{B} \right)^{\ast} \right)(g)
\end{align*}
が成り立つことを示せばよい。これはつまり
を示せばよい。
\begin{align*}
\pi_{X} \circ \pi_{X \times C} \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> \circ (f \times 1_{B \times C}) &= \pi_{X} \circ (f \times 1_{B \times C}) \\
&= f \circ \pi_{X}
\end{align*}
\begin{align*}
\pi_{X} \circ \pi_{X \times C} \circ \left( (f \times 1_{C}) \times 1_{B} \right) \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> &= \pi_{X} \circ (f \times 1_{C}) \circ \pi_{X \times C} \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> \\
&= f \circ \pi_{X} \circ \pi_{X \times C} \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> \\
&= f \circ \pi_{X}
\end{align*}
\begin{align*}
\pi_{C} \circ \pi_{X \times C} \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> \circ (f \times 1_{B \times C}) &= \pi_{C} \circ \pi_{B \times C} \circ (f \times 1_{B \times C}) \\
&= \pi_{C} \circ \pi_{B \times C}
\end{align*}
\begin{align*}
\pi_{C} \circ \pi_{X \times C} \circ \left( (f \times 1_{C}) \times 1_{B} \right) \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> &= \pi_{C} \circ (f \times 1_{C}) \circ \pi_{X \times C} \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> \\
&= \pi_{C} \circ \pi_{X \times C} \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> \\
&= \pi_{C} \circ \pi_{B \times C}
\end{align*}
\begin{align*}
\pi_{B} \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> \circ (f \times 1_{B \times C}) &= \pi_{B} \circ \pi_{B \times C} \circ (f \times 1_{B \times C}) \\
&= \pi_{B} \circ \pi_{B \times C}
\end{align*}
\begin{align*}
\pi_{B} \circ \left( (f \times 1_{C}) \times 1_{B} \right) \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> &= \pi_{B} \circ \left< \left< \pi_{X}, \pi_{C} \circ \pi_{B \times C} \right>, \pi_{B} \circ \pi_{B \times C} \right> \\
&= \pi_{B} \circ \pi_{B \times C}
\end{align*}
以上が成り立つことと product の UMP より が成り立つ。
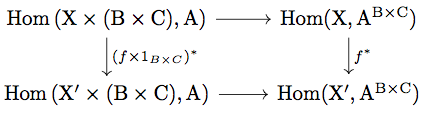
任意の と
に対して
\begin{align*}
\overline{f^{\ast}(\widetilde{g})} &= \overline{\widetilde{g} \circ f} \\
&= \epsilon \circ ( \widetilde{g} \circ f \times 1_{B \times C}) \\
&= \epsilon \circ (\widetilde{g} \times 1_{B \times C}) \circ (f \times 1_{B \times C}) \\
&= g \circ (f \times 1_{B \times C}) \\
&= (f \times 1_{B \times C})^{\ast}(g)
\end{align*}
が成り立つので、exponential の UMP より が成り立つ。
Proposition 8.6
上の証明と同様に証明できるので省略しますが、ここでは covariant 版の米田の埋め込みが使われていることに注意してください。
8.5 Limits in categories of diagrams
Proposition 8.7
ここでは が functor であること。またそれが
において limit となることの証明が省略されています。これらの事柄を確認しておきましょう。証明を考える前に Proposition 5.21 を復習して、任意の small category
と任意の functor
に関して
の limit が具体的にどのように構成されるかを再度確認しておいてください。
任意の に対して
で定義する。
次に任意の に対して次の diagram を考える。ただし
などは Proposition 5.21 と同様に定義されているとする。
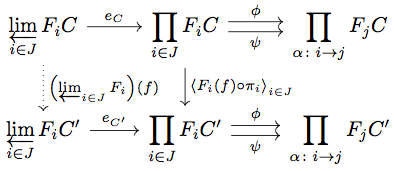
このとき任意の に対して
が natural transformation であるから以下の diagram が可換となる。
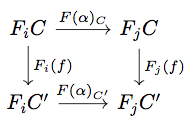
このことに注意すると
\begin{align*}
\pi_{\alpha} \circ \psi \circ \left< F_{i}(f) \circ \pi_{i} \right>_{i \in J} \circ e_{C} &= F(\alpha)_{C'} \circ \pi_{i} \circ \left< F_{i}(f) \circ \pi_{i} \right>_{i \in J} \circ e_{C} \\
&= F(\alpha)_{C'} \circ F_{i}(f) \circ \pi_{i} \circ e_{C} \\
&= F_{j}(f) \circ F(\alpha)_{C} \circ \pi_{i} \circ e_{C} \\
&= F_{j}(f) \circ \pi_{\alpha} \circ \psi \circ e_{C} \\
&= F_{j}(f) \circ \pi_{\alpha} \circ \phi \circ e_{C} \\
&= F_{j}(f) \circ \pi_{j} \circ e_{C} \\
&= \pi_{\alpha} \circ \phi \circ \left< F_{i}(f) \circ \pi_{i} \right>_{i \in J} \circ e_{C}
\end{align*}
が成り立つので、product の UMP より が成り立つ。よって equalizer の UMP より diagram を可換とするような
がただ一つ存在する。
そこで と定義する。
より
は functor の条件 (a) を満たす。
次に equalizer の UMP より が成り立つので、
は functor の条件 (b) を満たす。
最後に任意の と
に対して、
\begin{align*}
\pi_{i} \circ e_{C''} \circ \left( \varprojlim_{i \in J} F_{i} \right)(f \circ g) &= \pi_{i} \circ \left< F(f \circ g) \circ \pi_{i} \right>_{i \in J} \circ e_{C} \\
&= F(g) \circ F(f) \circ \pi_{i} \circ e_{C} \\
&= \pi_{i} \circ \left< F(g) \circ \pi_{i} \right>_{i \in J} \circ \left< F(f) \circ \pi_{i} \right>_{i \in J} \circ e_{C} \\
&= \pi_{i} \circ e_{C''} \circ \left( \varprojlim_{i \in J} F_{i} \right)(g) \circ \left( \varprojlim_{i \in J} F_{i} \right)(f)
\end{align*}
が成り立つので、product の UMP と equalizer の UMP より が成り立つ。よって
は functor の条件 (c) を満たす。
次に を任意の
に対して
で定義します。ここで
は上で
を定義する際に出てきたものとします。このとき
が
の limit となることを証明します。
はじめに が natural transformation となることを示す。
任意の に対して以下の diagram が可換になることを示せばよい。
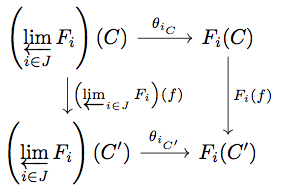
\begin{align*}
{\theta_{i}}_{C'} \circ \left( \varprojlim_{i \in J} F_{i} \right)(f) &= \pi_{i} \circ e_{C'} \circ \left( \varprojlim_{i \in J} F_{i} \right)(f) \\
&= \pi_{i} \circ \left< F_{i}(f) \circ \pi_{i} \right>_{i \in J} \circ e_{C} \\
&= F_{i}(f) \circ \pi_{i} \circ e_{C} \\
&= F_{i}(f) \circ {\theta_{i}}_{C}
\end{align*}
よって は natural transformation である。
次に任意の に対して
\begin{align*}
F(\alpha)(C) \circ {\theta_{i}}_{C} &= F(\alpha)(C) \circ \pi_{i} \circ e_{C} \\
&= \pi_{\alpha} \circ \psi \circ e_{C} \\
&= \pi_{\alpha} \circ \phi \circ e_{C} \\
&= \pi_{j} \circ e_{C} \\
&= {\theta_{j}}_{C}
\end{align*}
が成り立つので は diagram
の cone である。
最後に が limit であることを証明する。
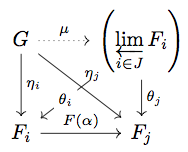
を diagram
の任意の cone とする。このとき Proposition 5.21 の議論にあるように、任意の
に対して
が成り立つので、
を満たす
がただ一つ存在する。このとき
が natural transformation となることを示す。
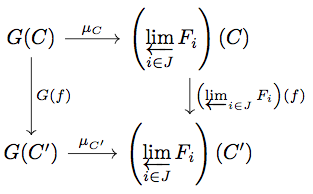
任意の と任意の
に対して
\begin{align*}
\pi_{i} \circ e_{C'} \circ \mu_{C'} \circ G(f) &= \pi_{i} \circ \left< {\eta_{i}}_{C'} \right>_{i \in J} \circ G(f) \\
&= {\eta_{i}}_{C'} \circ G(f) \\
&\underset{\eta_{i} \text{ is natural}}{=} F_{i}(f) \circ {\eta_{i}}_{C} \\
&= \pi_{i} \circ \left< F_{i}(f) \circ \pi_{i} \right>_{i \in J} \circ e_{C} \circ \mu_{C} \\
&= \pi_{i} \circ e_{C'} \circ \left( \varprojlim_{i \in J} F_{i} \right)(f) \circ \mu_{C}
\end{align*}
が成り立つので、product の UMP と equalizer の UMP より が成り立つ。
次に任意の が cone
から cone
への写像とすると任意の
と任意の
に対して
が成り立つので、product の UMP と equalizer の UMP より
が成り立つ。よって
は diagram
の limit である。
8.6 Colimits in categories of diagrams
Proposition 8.10
証明が省略されている箇所がいくつかあるので補っておきます。
任意の に対して米田の補題によって対応する natural transformation をここでは
と書くことにします。米田の補題の証明を見返して
の定義を再確認してください。
はじめに任意の に対して
が成り立つことを証明します。
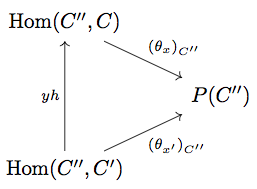
任意の と任意の
に対して
\begin{align*}
\left( (\theta_{x})_{C''} \circ yh \right)(f) &= P(h \circ f)(x) \\
&= \left( P(f) \circ P(h) \right)(x) \\
&= P(f)(x') \\
&= (\theta_{x'})_{C''}(f)
\end{align*}
次に を
で定義するとき、
が成り立つことを証明します。
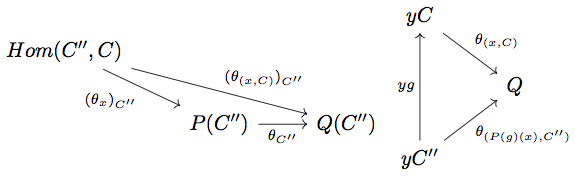
任意の に対して、
が cocone であることより上の右の diagram が可換になることに注意すると
\begin{align*}
\left( \theta_{C''} \circ (\theta_{x})_{C''} \right)(g) &= \theta_{C''} \left( P(g)(x) \right) \\
&= \left( \theta_{\left( P(g)(x), C'' \right)} \right)_{C''}(1_{C''}) \\
&= \left( (\theta_{(x, C)})_{C''} \circ \text{Hom}(-, g) \right)(1_{C''}) \\
&= (\theta_{(x, C)})_{C''}(g)
\end{align*}
が成り立つ。
次に が natural transformation であることを証明します。
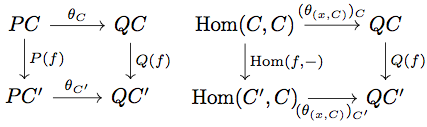
任意の と任意の
に対して、
が natural transformation であるから上の右の diagram が可換になることに注意すると
\begin{align*}
\left( Q(f) \circ \theta_{C} \right)(x) &= \left( Q(f) \circ ( \theta_{(x, C)})_{C} \right)(1_{C}) \\
&= \left( (\theta_{(x,C)})_{C'} \circ \text{Hom}(f, -) \right)(1_{C}) \\
&= (\theta_{(x,C)})_{C'}(f)
\end{align*}
が成り立つ。一方先程の証明と同様に が成り立つことに注意すると
\begin{align*}
\left( \theta_{C'} \circ P(f) \right)(x) &= (\theta_{\left( P(f)(x), C' \right)})_{C'}(1_{C'}) \\
&= \left( (\theta_{(x, C)})_{C'} \circ \text{Hom}(-, f) \right)(1_{C'}) \\
&= (\theta_{(x, C)})_{C'}(f)
\end{align*}
が成り立つ。
最後に が unique に決まることを証明します。
任意の に対して
\begin{align*}
\varphi_{C}(x) &= \left( \varphi_{C} \circ (\theta_{x})_{C} \right)(1_{C}) \\
&= (\varphi \circ \theta_{x})_{C}(1_{C}) \\
&= (\theta_{(x,C)})_{C}(1_{C}) \\
&= \theta_{C}(x)
\end{align*}
が成り立つので である。
8.7 Exponentials in categories of diagrams
ここでは が cocone となることの証明が省略されていますが、これは簡単なので確認しておいてください。
次の が isomorphism であることを証明する箇所で
が集合であるとみなしてよいという点がわかりにくいかもしれません。
Propostiion 8.7 や 8.8 の議論から functor category においては limit や colimit は pointwise に定義されるのでした。そこで の domain と codomain を展開すると
となります。
や
は集合です。そこで、
の部分を書くのを省略して(記号を乱用して)
を初めから集合とみなして考えましょうということです。
書籍では covariant 版の米田の補題を用いて を証明するという方針がとられています。証明では同型射であることは示されていますが、
に関して natural であることの証明が省略されているので、これを補っておきます。
まず、任意の に対して
を証明します。
Proposition 5.21 の議論から colimit は以下の diagram によって具体的に構成される。
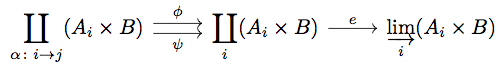
Corollary 5.27 より contravariant representable functor によって全ての colimit は limit に移されることに注意して以下の diagram を考える。
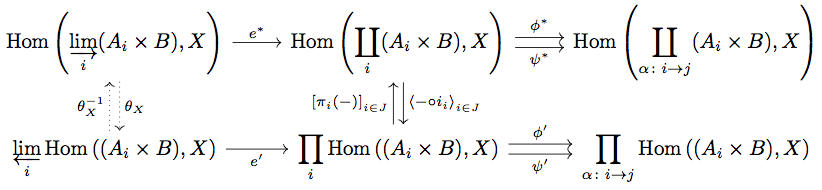
ここで を
と表すとすると、
はそれぞれ
を満たす。
の定義
任意の に対して、
が成り立つ。よって
が成り立つことに注意すると、
\begin{align*}
(\pi_{\alpha} \circ \phi' \circ \left< - \circ i_{i} \right>_{i \in J} \circ e^{\ast})(f) &= \pi_{i} \circ \left< f \circ e \circ i_{i} \right>_{i \in J} \\
&= f \circ e \circ i_{i} \\
&= f \circ e \circ i_{j} \circ (A \times B)(\alpha) \\
&= (A \times B)(\alpha)^{\ast} \circ \pi_{j} \circ \left< f \circ e \circ i_{i} \right>_{i \in J} \\
&= (\pi_{\alpha} \circ \psi' \circ \left< - \circ i_{i} \right>_{i \in J} \circ e^{\ast})(f)
\end{align*}
が成り立つ。よって product の UMP と equalizer の UMP より を満たすただ一つの
が存在する。
の定義
任意の に対して、
であることに注意すると、
\begin{align*}
\left[ \pi_{i} \left( e'(g) \right) \right]_{i \in J} \circ \phi \circ i_{\alpha} &= \left[ \pi_{i} \left( e'(g) \right) \right]_{i \in J} \circ i_{i} \\
&= \pi_{i} \left( e' (g) \right) \\
&= (\pi_{\alpha} \circ \phi' \circ e')(g)
\end{align*}
同様に、
\begin{align*}
\left[ \pi_{i} \left( e'(g) \right) \right]_{i \in J} \circ \psi \circ i_{\alpha} &= \left[ \pi_{i} \left( e'(g) \right) \right]_{i \in J} \circ i_{j} \circ (A \times B)(\alpha) \\
&= \pi_{j} \left( e'(g) \right) \circ (A \times B)(\alpha) \\
&= (\pi_{\alpha} \circ \psi' \circ e')(g)
\end{align*}
が成り立つ。よって であるから、coproduct の UMP と equalizer の UMP より
を満たすただ一つの
が存在する。
が isomorphism であること
、
が成り立つことは product の UMP、coproduct の UMP より容易に証明できる。
よって equalizer の UMP より かつ
が成り立つので、
は isomorphism である。
次に が natural in X であることを証明します。任意の
に対して
がどのように定義されるかは Proposition 8.7 の証明を参照してください。
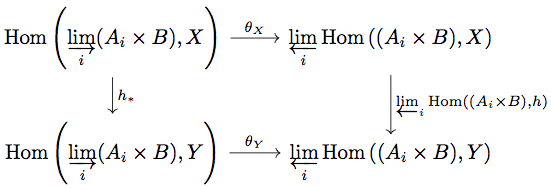
任意の と任意の
に対して、
\begin{align*}
\left( \pi_{i} \circ e'_{Y} \circ \varprojlim_{i} \text{Hom} \left((A_{i} \times B), h \right) \circ \theta_{X} \right)(f) &= \left( \pi_{i} \circ \left< \text{Hom}\left( (A_{i} \times B), h \right) \circ \pi_{i} \right>_{i \in J} \circ e'_{X} \circ \theta_{X} \right)(f) \\
&= \left( \text{Hom} \left( (A_{i} \times B), h \right) \circ \pi_{i} \circ \left< - \circ i_{i} \right>_{i \in J} \circ e^{\ast} \right)(f) \\
&= h \circ f \circ e \circ i_{i}
\end{align*}
一方で
\begin{align*}
(\pi_{i} \circ e'_{Y} \circ \theta_{Y} \circ h_{\ast})(f) &= \left( \pi_{i} \circ \left< - \circ i_{i} \right>_{i \in J} \circ e^{\ast} \circ h_{\ast} \right) (f) \\
&= h \circ f \circ e \circ i_{i}
\end{align*}
が成り立つ。よって product の UMP と が monic であることより
は natural transformation となる。
任意の に対して
は exponential の UMP より成り立ちます。このとき、
が成り立つことは自明でしょうか?
証明は上の証明とほとんど同じなので概略だけ示しておきます。
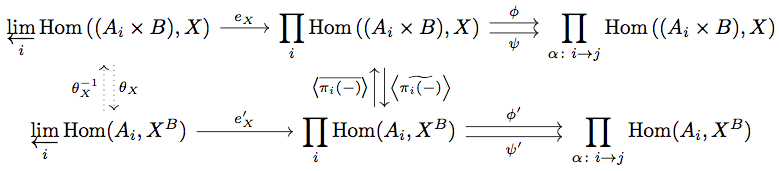
上の証明と同様に diagram を可換とするような と
が equalizer の UMP よりただ一つ存在する。
と
は明らかに逆射となるので equalizer の UMP により
は isomorphism である。
次に が natural transformation となることを証明します。任意の
に対して
がどのように定義されるのか Proposition 6.7 の証明をみて再確認してください。
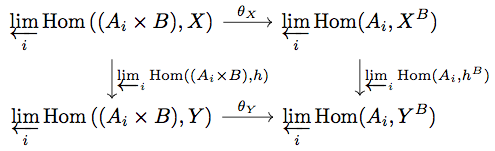
任意の に対して、
\begin{align*}
\left( \pi_{i} \circ e'_{Y} \circ \varprojlim_{i} \text{Hom} (A_{i}, h^{B}) \circ \theta_{X} \right)(f) &= \left( \pi_{i} \circ \left< \text{Hom}(A_{i}, h^{B}) \circ \pi_{i}(-) \right>_{i \in J} \circ e'_{X} \circ \theta_{X} \right)(f) \\
&= \left( \text{Hom}(A_{i}, h^{B}) \circ \pi_{i} \circ \left< \widetilde{\pi_{i}(-)} \right>_{i \in J} \circ e_{X} \right)(f) \\
&= h^{B} \circ \widetilde{\pi_{i} \left( e_{X}(f) \right)}
\end{align*}
が成り立つ。また、
\begin{align*}
\left( \pi_{i} \circ e'_{Y} \circ \theta_{Y} \circ \varprojlim_{i} \text{Hom} \left( (A_{i} \times B), h \right) \right)(f) &= \left( \pi_{i} \circ \left< \widetilde{ \pi_{i}(-) } \right>_{i \in J} \circ e_{Y} \circ \varprojlim_{i} \text{Hom} \left( (A_{i} \times B), h \right) \right)(f) \\
&= \left( \widetilde{ \pi_{i}(-) } \circ \left< \text{Hom} \left( (A_{i} \times B), h \right) \circ \pi_{i}(-) \right>_{i \in J} \circ e_{X} \right)(f) \\
&= \widetilde{h \circ \pi_{i} \left( e_{X}(f) \right)}
\end{align*}
が成り立つ。一方
\begin{align*}
eval_{Y} \circ \left( h^{B} \circ \widetilde{\pi_{i} \left( e_{X}(f) \right)} \times 1_{B} \right) &= eval_{Y} \circ ( h^{B} \times 1_{B}) \circ \left( \widetilde{ \pi_{i} \left( e_{X}(f) \right)} \times 1_{B} \right) \\
&= h \circ eval_{X} \circ \left( \widetilde{ \pi_{i} \left( e_{X}(f) \right)} \times 1_{B} \right) \\
&= h \circ \pi_{i} \left( e_{X}(f) \right)
\end{align*}
が成り立つので、exponential の UMP と product の UMP より が成り立つ。
上の証明でわかるように natural transformation になることの証明が非常に面倒です。より簡単な証明はないのでしょうか?
今考えている圏が であることを利用すると、もっと直接的に
を示すことができます。
ここでは の要素を
と表します。
を
で定義する。すると
が isomorphism となることは明らかである。このとき以下の diagram を考える。
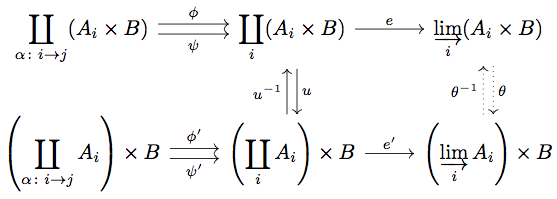
任意の に対して
が成り立つので coequalizer の UMP より diagram を可換とする
がただ一つ存在する。同様に
がただ一つ存在して、
が isomorphism であるから coequalizer の UMP より
は isomorphism となる。
Theorem 8.14
証明するべきことは と
です。
natural isomorphism を構成すればよい。任意の
に対して
を任意の
に対して
で定義する。すると product の UMP より
は isomorphism となる。
次にこの が
に関して natural であることを示す。
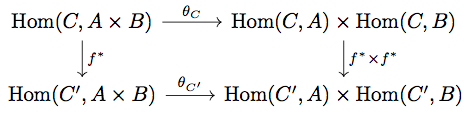
任意の と任意の
に対して、
が成り立つ。
任意の に対して
\begin{align*}
y(A^{B})(C) = \text{Hom}(C, A^{B}) &\cong \text{Hom}(C \times B, A) \\
&= yA(C \times B) \\
&\cong \text{Hom} \left( y(C \times B), yA \right) \\
&\cong \text{Hom} ( yC \times yB, yA ) = yA^{yB}(C)
\end{align*}
が成り立つので、この isomorphism を とする。このとき
が
に関して natural であることを示せばよい。
その証明は今までの証明と同様なので省略する。
Theorem 8.14 は contravariant 版の米田の埋め込みに対しての定理ですが、covariant 版の米田の埋め込みに関してはどのようなことが成り立つでしょうか?考えて、証明してみてください。
8.8 Topoi
Proposition 8.18
書籍で の定義が与えられていますが、この表記はわかりにくいです。より正確には、
とすると任意の
に対して
と定義されます。
このとき、 が sieve となること、つまり precomposition に対して閉じていることを確認する必要があります。さらに pullback condition に関しても証明する必要があります。
任意の と任意の
に対して、
が存在して
となることを示せばよい。
より、
が存在して
が成り立つ。 一方で
が natural transformation であることより
が成り立つことに注意すると、
が成り立つ。
よって とすれば、
となるので
は sieve である。
任意の が
を満たすとする。このとき natural transformation
がただ一つ存在して
を満たすことを示せばよい。
任意の と任意の
に対して
が total sieve であることより、
が成り立つ。言い換えると
が存在して
が成り立つ。そこで
と定義する。このとき
が成り立つ。
次に、任意の に対して
\begin{align*}
\theta_{C'} \circ U(f) \circ \alpha_{C} &= E(f) \circ \theta_{C} \circ \alpha_{C} \\
&= E(f) \circ \phi_{C} \\
&= \phi_{C'} \circ X(f) \\
&= \theta_{C'} \circ \alpha_{C'} \circ X(f)
\end{align*}
が成り立つ。 は monic であるから、
が成り立つ。よって
は natural transformation である。
最後に を diagram を可換とするような natural transformation であるとする。
すると任意の に対して
が成り立つが、
は monic であるから、
となる。よって
となる。
参考書籍

Category Theory (Oxford Logic Guides)
- 作者:Awodey, Steve
- 発売日: 2008/01/10
- メディア: ペーパーバック

- 作者:スティーブ アウディ
- 発売日: 2015/09/19
- メディア: 単行本