Steve Awodey の Category Theory を読む シリーズトップ
- 10.2 Monads and adjoints
- 10.3 Algebras for a monad
- 10.4 Comonads and coalgebras
- 10.5 Algebras for endofunctors
- 参考書籍
10.2 Monads and adjoints
Example 10.5
Exercise 6 と同様の表記を採用すると、任意の と任意の
に対して
と表せる。また任意の
に対して
と表せることに注意して以下を証明する。
\begin{align*}
(\mathcal{P}, \{-\}, \bigcup) \text{ is a monad on } {\bf{Sets}}.
\end{align*}
が natural であること
任意の に対して以下の diagram を考える。
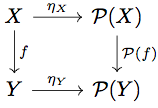
すると、任意の に対して
が成り立つ。よって diagram は可換になる。
が natural であること
任意の に対して以下の diagram を考える。
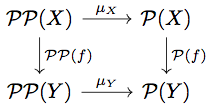
任意の に対して
\begin{align*}
\left( \mathcal{P}(f) \circ \mu_{X} \right)(\alpha) &= \mathcal{P}(f) \left( \left\{ x \in X \,\middle|\, \exists U \in \alpha,\, x \in U \right\} \right) \\
&= \left\{ f(x) \in Y \,\middle|\, \exists U \in \alpha,\, x \in U \right\}
\end{align*}
が成り立つ。一方、
\begin{align*}
\left( \mu_{Y} \circ \mathcal{PP}(f) \right)(\alpha) &= \mu_{Y} \left( \left\{ \mathcal{P}(f)(U) \,\middle|\, U \in \alpha \right\} \right) \\
&= \left\{ y \in Y \,\middle|\, \exists U' \in \left\{ \mathcal{P}(f)(U) \,\middle|\, U \in \alpha \right\},\, y \in U' \right\} \\
&= \left\{ y \in Y \,\middle|\, \exists U \in \alpha,\, y \in \mathcal{P}(f)(U) \right\} \\
&= \left\{ y \in Y \,\middle|\, \exists U \in \alpha,\, y \in \left\{ f(x) \in Y \,\middle|\, x \in U \right\} \right\} \\
&= \left\{ f(x) \in Y \,\middle|\, \exists U \in \alpha,\, x \in U \right\}
\end{align*}
が成り立つ。よって diagram は可換になる。
- 結合則を満たすこと
任意の に対して以下の diagram が可換になることを示せばよい。
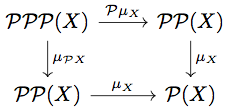
任意の に対して
\begin{align*}
\left( \mu_{X} \circ \mathcal{P}\mu_{X} \right)(\beta) &= \mu_{X} \left( \left\{ \mu_{X}(\alpha) \,\middle|\, \alpha \in \beta \right\} \right) \\
&= \left\{ x \in X \,\middle|\, \exists U \in \left\{ \mu_{X}(\alpha) \,\middle|\, \alpha \in \beta \right\},\, x \in U \right\} \\
&= \left\{ x \in X \,\middle|\, \exists \alpha \in \beta,\, x \in \mu_{X}(\alpha) \right\} \\
&= \left\{ x \in X \,\middle|\, \exists \alpha \in \beta,\, U \in \alpha,\, x \in U \right\}
\end{align*}
が成り立つ。一方、
\begin{align*}
\left( \mu_{X} \circ \mu_{\mathcal{P}X} \right)(\beta) &= \mu_{X} \left( \left\{ U \in \mathcal{P}(X) \,\middle|\, \exists \alpha \in \beta,\, U \in \alpha \right\} \right) \\
&= \left\{ x \in X \,\middle|\, \exists U' \in \left\{ U \in \mathcal{P}(X) \,\middle|\, \exists \alpha \in \beta,\, U \in \alpha \right\},\, x \in U' \right\} \\
&= \left\{ x \in X \,\middle|\, \exists \alpha \in \beta,\, U \in \alpha,\, x \in U \right\}
\end{align*}
が成り立つので diagram は可換になる。
- 単位則を満たすこと
任意の に対して以下の diagram が可換になることを示せばよい。
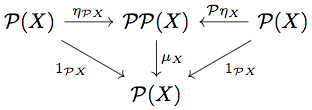
任意の に対して左の triangle に関して
\begin{align*}
\left( \mu_{X} \circ \eta_{\mathcal{P}X} \right)(U) &= \mu_{X} \left( \left\{ U \right\} \right) \\
&= \left\{ x \in X \,\middle|\, \exists U' \in \left\{ U \right\},\, x \in U' \right\} \\
&= U
\end{align*}
が成り立つ。次に右の triangle に関して
\begin{align*}
\left( \mu_{X} \circ \mathcal{P}\mu_{X} \right)(U) &= \mu_{X} \left( \left\{ \left\{ x \right\} \,\middle|\, x \in U \right\} \right) \\
&= \left\{ x' \in X \,\middle|\, \exists U' \in \left\{ \left\{ x \right\} \,\middle|\, x \in U \right\},\, x' \in U' \right\} \\
&= \left\{ x \in X \,\middle|\, x \in U \right\} \\
&= U
\end{align*}
が成り立つので diagram は可換になる。
10.3 Algebras for a monad
Example 10.7
free monoid adjunction に対する monad を とすると、
が成り立つことを示します。
はじめに を定義する。
任意の monoid に対して
と定義する。ただし
は
を満たす関数とする。このとき書籍にあるように
は
-algebra となる。
また任意の monoid homomorphism に対して以下の diagram を考える。
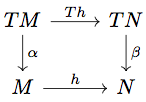
任意の に対して
が成り立つ。一方、
が成り立つが
が monoid homomorphism であることから両者は等しい。
そこで で定義する。すると
が functor の条件を満たすことは明らかである。
次に を定義する。
任意の に対して
、
とするとき、
で定義する。このとき
が monoid となることを示す。
任意の に対して
一方、
が成り立つので、 は結合則を満たす。また
が成り立つ。同様に が成り立つので
は 単位則を満たす。以上より
は monoid となる。
また任意の と任意の
に対して、
が成り立ち、同様に が成り立つので、
は monoid homomorphism となる。そこで
とすれば
は明らかに functor の条件を満たす。
最後に、 かつ
が成り立つので
が成り立つ。
10.4 Comonads and coalgebras
任意のadjoint pair に対して unit を
、counit を
とするとき、
が comonad となることを確認します。
10.2 節と同様に証明する。
- coassociativity law が成り立つこと
任意の に対して
が natural であることより、以下の diagram が可換になる。
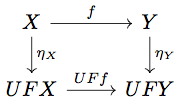
を
、
を
で置き換えると、以下の diagram を得る。
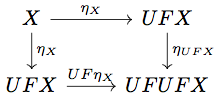
を
として、全体に
を適用すると以下の diagram を得る。
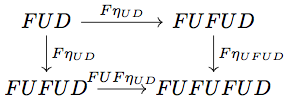
記号を置き換えると以下の diagram が可換となる。
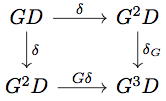
- counit law が成り立つこと
次の diagram が可換になることを示せばよいが、これは triangle identities より明らかである。
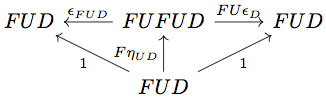
10.5 Algebras for endofunctors
Lemma 10.10
任意の endofunctor に関して次の事柄が成り立つことを証明します。
が initial
-algebra であることより、次の diagram が可換となるような
がただ一つ存在する。
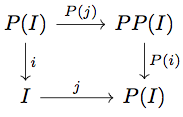
そこで以下の diagram を考える。
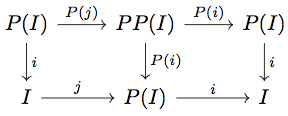
明らかに diagram は可換になるので、 が initial であることより
が成り立つ。
そこでもう一度以下の diagram を考えると
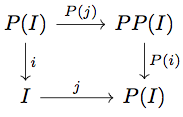
が成り立つ。よって
は isomorphism である。
Corollary 10.13
任意の finite polynomial functor が
-colimit を保存することを証明します。
index category に対しては
が成り立つこと、また、任意の集合 に対しては
が成り立つことに注意する。
polynomial functor を
で表すと、任意の
に対して、証明するべきことは
である。
任意の に対して
\begin{align*}
\text{Hom}\left( \sum_{I} C_{i} \times \left( \varinjlim_{n} D_{n} \right)^{B_{i}}, X \right) &\cong \text{Hom} \left( C_{i} \times \left(\varinjlim_{n} D_{n} \right)^{B_{i}}, \Delta_{I} X \right) \\
&\cong \text{Hom} \left( \left(\varinjlim_{n} D_{n} \right)^{B_{i}}, \Delta_{I} X^{C_{i}} \right) \\
&\cong \text{Hom} \left( \varinjlim_{n} D_{n}^{B_{i}}, \Delta_{I} X^{C_{i}} \right) \\
&\cong \varprojlim_{n} \text{Hom} \left( D_{n}^{B_{i}}, \Delta_{I} X^{C_{i}} \right) \\
&\cong \varprojlim_{n} \text{Hom} \left( C_{i} \times D_{n}^{B_{i}}, \Delta_{I} X \right) \\
&\cong \varprojlim_{n} \text{Hom} \left( \sum_{I} C_{i} \times D_{n}^{B_{i}}, X \right) \\
&\cong \text{Hom} \left( \varinjlim_{n} \left( \sum_{I} C_{i} \times D_{n}^{B_{i}} \right), X \right) \\
\end{align*}
が成り立つ。これらの同型射は adjoint pair の同型射であるから Chapter8 で証明した内容と合わせると に関して natural である。
よって米田の補題より が成り立つ。
参考書籍

Category Theory (Oxford Logic Guides)
- 作者:Awodey, Steve
- 発売日: 2008/01/10
- メディア: ペーパーバック

- 作者:スティーブ アウディ
- 発売日: 2015/09/19
- メディア: 単行本