ナンプレ(数独)は難しさを定義するのが難しい

はじめに
仮置きは最強のテクニックだけど邪道です
世界一難しいナンプレの問題の作成に失敗
ナンプレを解くための 13 個のテクニック
ナンプレの難しさを定義する
まだ発展・改良の余地はあるか？
おわりに
補足: 技術的な話

はじめに

私は先日、最新技術にキャッチアップするためにレベル別ナンプレ(数独) – 無料問題集 | パズル製作研究所（以下 puzzle.dev）というナンプレのサイトを構築しました。サイトでは自動生成した大量の問題の中から毎日難易度順に 13 問をランダムに出題しています。

以前、 CalcBlocks というサイトで計算ブロック・数字ブロック・ビルディングパズルなどのナンプレよりも自動生成が難しいパズルの自動生成をしていたのでナンプレサービスも簡単に作れるだろうと思ってました。

確かに、ナンプレの問題の自動生成はすぐにできました。でも、難易度別に問題を出し分けようとした時、問題に直面しました。

ナンプレの難しさって何で決まるんだ？

サイトを作り始めた頃は初期のヒントの数が少ないほど難しいと思っていましたが、これは間違いです。私はあまりにもナンプレのことを知らなさ過ぎました。

この記事は、以前の私と同様にナンプレというパズルの存在やルール位は知っているけど、解き方のテクニックなどについては詳しく知らない人向けにナンプレの奥深さを知ってもらいたくて書きました。
まず、初心者の多くが使う仮置きという解き方テクニックについて説明します。次に、世界一難しいナンプレの問題を作ろうとして失敗した話を紹介します。最後に、私がナンプレを解くテクニックを 13 個に整理してそれを使って難易度を定義した話をします。

仮置きは最強のテクニックだけど邪道です

puzzle.dev を作る前の私はナンプレについて

電車やバスでおじさんが解いてる時間をかけさえすれば簡単に解けるパズル

程度の認識でした。時間をかけさえすれば解くことができるというのは正しいです。仮置きと呼ばれるテクニックをひたすら繰り返せば原理的には解けます。
仮置きは以下のようなテクニックです。

数字が確定できるセルに数字をすべて入れる
数字が確定していないセルに入る可能性がある数字の中から適当に数字を入れる
1 と 2 をナンプレのルールと矛盾する、もしくは答えにたどり着くまで繰り返す
ナンプレのルールと矛盾したら、2 に戻って別の数字を試す

仮置きはどんなナンプレの問題もこのテクニックだけで解くことができる最強で汎用性の高いテクニックです。ナンプレを解くプログラムを作成しろと言われたらほとんどのプログラマーはこのアルゴリズムを実装しようとするのではないでしょうか？
一方で、このアルゴリズムは、矛盾にたどり着いた場合にはさかのぼって別の数字を試すという BackTrack（引き戻し）が何度も発生するので紙の上で人が実行するのはほとんど不可能です。アプリ等で補助を受けても難しいし単なる運ゲーになってしまって楽しくありません。
これらの理由からナンプレ愛好家の間では仮置きは邪道と見なされています。

世界一難しいナンプレの問題の作成に失敗

10 年ほど前、世界一難しいナンプレの問題を作ったと数学者が発表したのち、その問題がすぐに基本的なテクニックのみを用いて解かれたことがありました。当時の様子は以下の記事で伺い知ることができます。

ここは推測なのですが、おそらく仮置きのアルゴリズムをベースに難しさを定義していたのではないかと思います。しかし、すでに述べたようにナンプレ愛好家は仮置きを使いません。特定のアルゴリズムを使ってコンピューターで解くのが難しくても、人間が簡単に解けるならその問題は難しいと言えるでしょうか。

私は当初、初期のヒントの数が少なければ少ないほど難しいのではないかと考えていましたが、初期のヒントの数が少なくても基本的なテクニックのみで解ける問題はたくさんあります。初期のヒントが少ない問題を作るのはとても難しいです。でも、人間が簡単に解けるならやはり難しい問題とは言えないと思います。
ちなみに、ナンプレの問題の初期のヒントの最小個数は 17個であることが知られています。

大切なのは人間にとっての難しさです。

ナンプレを解くための 13 個のテクニック

人間にとっての難しさを定義するためには、ナンプレ愛好家の人たちがナンプレを解く時に使用しているテクニックについて十分によく理解する必要があります。
ナンプレを解くテクニックには大きく分けて 2 つの種類があります。

この空白のセルにはこの数字しか入らないと決めるテクニック
この空白のセルにはこの数字は入らないと決めるテクニック

ほとんどのナンプレ初心者の方は空白のセルに入る数字の候補を減らしていく 2 つ目の種類のテクニックを知らないために難しい問題を解くことができないと思います。
ナンバープレース(ナンプレ、数独)の解き方テクニック集 | パズル製作研究所では下の 13 個のテクニックについて図を使いながら詳しく解説しました。

13 個のテクニックは、私が書籍やネットで公開されているテクニックを調べて、それぞれについてそれは一体どういうテクニックなのか、他のテクニックとどう関係しているのか、新しいテクニックはないかなどを検討して整理した結果です（名前は適当です）。
例えばテクニック4 の 3 人寄ればもんじゅの知恵は私のオリジナルのテクニックです(私が知らないだけでどこかで解説されているかもしれません)。
他にもテクニック7 の隠しレーザーはよく知られたテクニックですが、そのテクニックを少し変更したテクニック8 の隠しコレーザーを説明しているサイトはほとんどありません。
テクニック 1 から 6 がこの数字しか入らないと決めるテクニックで、テクニック 7 以降がこの数字は入らないと決めるテクニックです。

AWS 上でランダムに作成した 4000 万問のナンプレの問題を実際に 13 個のテクニックを使用して解いたところ 99.5% の問題を解くことができました。逆に言うと、0.5% の問題は解くことができませんでした。
この結果から、私が解説したテクニックの集合は完全ではないにせよ十分に強力だと考えています。

ナンプレの難しさを定義する

人間にとっての難しさを定義する準備が整いました。
puzzle.dev では 13 個のテクニックを上で紹介した順で簡単なテクニックから難しいテクニックの順に並べています。その上で、より難しいテクニックを多く使わないと解けない問題の方が難しいと定義しています。

もう少し正確に定義します。
問題を解く場合には必ず簡単なテクニックから試します。もし、使えるテクニックが見つかればそのテクニックを使って、セルに入る数字を決めるか、セルに入る数字の候補を減らします。次は、再度最初のテクニックに戻って使えるテクニックを探します。これを繰り返します。
この手順にしたがって問題を解くと、それぞれのテクニックを使った回数が得られます。例えばテクニック 1 からテクニック 13 の順に使った回数を並べると次のようになります。
\begin{align*}
[21,24,0,0,1,0,0,0,0,0,0,0,0]
\end{align*}
これはある問題を解くのに、テクニック 1 を 21 回、テクニック 2 を 24 回、テクニック 5 を 1 回使ったことを表しています。どの順でテクニックを使ったかはわかりません。
難易度を決める際には先ほどのテクニックの使用回数を逆順に並べ替えた後で辞書式順序で比較します。例えば問題を解くのに使ったテクニックの回数が以下の 2 つの問題があったとします。
\begin{align*}
\text{問題} 1: [21,24,0,0,1,0,0,0,0,0,0,0,0] \\
\text{問題} 2: [21,22,1,1,0,1,0,0,0,0,0,0,0]
\end{align*}
この二つの問題の難しさを比較するためにこの数字の並び順をそれぞれ逆順に並べ替えます。
\begin{align*}
[0,0,0,0,0,0,0,0,1,0,0,24,21] \\
[0,0,0,0,0,0,0,1,0,1,1,22,21]
\end{align*}
この二つを辞書式順序で比較します。すると、
\begin{align*}
[0,0,0,0,0,0,0,0,1,0,0,24,21] \lt [0,0,0,0,0,0,0,1,0,1,1,22,21]
\end{align*}
となるので、この順序で大きい問題 2 が問題 1 より難しい問題であると判断します。
この難易度の決め方によって「より難しいテクニックをより多く使っている問題の方が難しい問題である」という気持ちを順序として表現することができます。

まだ発展・改良の余地はあるか？

puzzle.dev では、ナンプレの難易度の定義をより難しいテクニックを使わないと解けない問題の方が難しいと定義しましたが、これは唯一絶対正しい難易度の定義ではありません。例えば XY チェインやシンプルチェインの長さは現状一切考慮していませんが、チェインの長さが長い方が難しい問題になると思います。より人間の感覚に合うように難しさの定義も修正していく必要があります。

自動生成した問題のうち 0.5% の問題は 13 個のテクニックを利用しても解けません。13 個のテクニックを適用できない状況を詳しく分析することで新しいテクニックを発見できる可能性があります。新しいテクニックが見つかれば、難しさの定義も変える必要があります。

私が思いもつかないようなテクニックや、難易度の定義をみなさんが思いついてくれることを楽しみにしています。

おわりに

この記事を読んでナンプレの奥深さを知って楽しんでくれる人が増えると嬉しいです。

補足: 技術的な話

補足としてナンプレの問題の自動生成に用いた技術について簡単に解説します。

サイトを支える技術

サイトの構成には以下のフレームワークやサービスを使用しました。

Reactベース静的サイトジェネレータ GatsbyJS
Headless CMS の Contentful
認証プラットフォームの Auth0
Firebase Hosting

サーバー側は AWS 上で APIGateway + Lambda のサーバーレスで構築しています。
ナンプレの問題の自動生成も Lambda 関数の組み合わせで実現し構成は全て Terraform で管理しています。

Sat Solver を利用した問題の自動生成

ここでは初期のヒントからナンプレのルールを満たす答えがただ一つに決まる問題を正当な問題と呼びます。
問題を自動生成するにあたりナンプレを解くプログラムは次の 2 種類必要です。

人間が使うテクニックを使って問題を解くプログラム
初期のヒントからナンプレのルールを満たす全ての答えを探索するプログラム

1 つ目のプログラムは自動生成した問題の難易度の判定に使用します。ただし、このプログラムは初期のヒントを満たす答えが複数個ある場合に、その一つしか見つけられない可能性があります。答えが複数個存在する問題は正当なナンプレの問題とみなされないので確実に判別して取り除く必要があります。また、上で述べたように、正当な問題であっても 0.5% の問題は解けません。正当な問題を解けない場合があると、初期のヒントとナンプレのルールを満たす答えがそもそも存在しないのか、単にこのプログラムで解けないだけなのか判別できません。よって、このプログラムだけで自動生成をすることはできません。

そこで 2 つ目のプログラムを用意します。このプログラムに必要な要件は次の 2 つです。

正当な問題はすべて解くことができる
初期のヒントとナンプレのルールを満たす答えを全て見つけることができる

puzzle.dev ではこれらの要件を満たすプログラムの実装に Sat Solver と呼ばれるソフトウェアを使用しています。

Sat Solver の使用場所

Sat Solver 自体について説明する前に Sat Solver の使用場所を下の図に従って説明します。

まず 1 のナンプレのルールを満たす数字の配置を探索する際に Sat Solver を使用しています。ちなみに、ナンプレのルールを満たす数字の配置は 6,670,903,752,021,072,936,960通りあるそうです（参考: ■数独の解は何通りか？: ガスコン研究所）。
次に、ヒントとなる数字を配置が点対称になるようにピックアップします。ヒントの配置が何かしらの対称性を持っているのはナンプレ業界の暗黙の了解でヒントの配置にこだわる人もいます。
最後に、もう一度 Sat Solver を使用してヒントとナンプレのルールを満たす全ての答えを探索します。図では赤い数字の位置が異なる 2 つの答えが見つかります。これは正当な問題ではないので、再度 2 のヒントのピックアップからやり直します。答えが 1 つしかない問題が見つかれば正当な問題として採用します。

Sat Solver とは

Sat Solver は充足可能性問題を高速に解くことに特化したプログラムです。
充足可能性問題とは、変数と、否定 $\lnot$ 、論理和 $\lor$ 、論理積 $\land$ から構成される論理式を与えらえれた時に、論理式全体を True にするような変数の True もしくは False の割り当てが存在するかどうかを問う問題です。
私が使用した Sat Solver の実装のひとつ MiniSat は論理式を連言標準形で受け取ります。連言標準形は以下のように構成されます。

変数 $x$ ，またはその否定 $\lnot x$ をリテラルと呼ぶ
リテラルを論理和 $\lor$ で結合した論理式を節と呼ぶ
節を論理積 $\land$ で結合した論理式を連言標準形と呼ぶ

例えば、以下の論理式は連言標準形の例です。
\begin{align*}
\lnot x_{0} \land (x_{1} \lor x_{2})
\end{align*}
この論理式に対しては
\begin{align*}
[ x_{0} \mapsto \rm{False},\, x_{1} \mapsto \rm{True},\, x_{2} \mapsto \rm{True}]
\end{align*}
などが論理式を充足する割り当てです。Sat Solver はこのような変数への割り当てを高速に求めます。
Sat Solver の実装について興味がある方は以下の書籍が参考になるでしょう。

The Art of Computer Programming, Volume 4, Fascicle 6: Satisfiability (English Edition)

作者:Knuth, Donald E.
発売日: 2016/04/19
メディア: Kindle版

ナンプレに限定すると、Sat Solver は上で説明した仮置きを高速に非常に効率よく実行していると考えられます。

ナンプレのルールを連言標準形で表現する

いくつかの用語を説明なしに使用するので用語の説明で確認してください。

ナンプレを Sat Solver で解くためにはナンプレのルールを連言標準形で表現する必要があります。ナンプレのルールを確認しておきます。

各セルには数字が 1 つ入ります。
各行には 1 から 9 の各数字が 1 度ずつ入ります。
各列には 1 から 9 の各数字が 1 度ずつ入ります。
太い線で囲まれた各 3x3 の枠内には 1 から 9 の各数字が 1 度ずつ入ります。
正解は1つだけです。

ルール 1 を連言標準形の形に変換します。
座標が (1, 1) のセルについて考えます。このセルには 1 から 9 の数字が 1 つ入ります。そこで、このセルの数字に対応する変数として 9 つの変数を用意します。
\begin{align*}
q_{1_{(1,1)}},\, q_{2_{(1,1)}},\, q_{3_{(1,1)}},\, q_{4_{(1,1)}},\, q_{5_{(1,1)}},\, q_{6_{(1,1)}},\, q_{7_{(1,1)}},\, q_{8_{(1,1)}},\, q_{9_{(1,1)}}
\end{align*}
この 9 つの変数の中で True が割り当てられた変数に対応する数字がこのセルに入ると解釈します。例えば、以下のような割り当てを Sat Solver がした場合は、数字の 3 がセルに入ると解釈します。
\begin{align*}
[ q_{1_{(1,1)}} \mapsto \rm{False},\, q_{2_{(1,1)}} \mapsto \rm{False},\, q_{3_{(1,1)}} \mapsto \rm{True},\, q_{4_{(1,1)}} \mapsto \rm{False},\, q_{5_{(1,1)}} \mapsto \rm{False},\\
q_{6_{(1,1)}} \mapsto \rm{False},\, q_{7_{(1,1)}} \mapsto \rm{False},\, q_{8_{(1,1)}} \mapsto \rm{False},\, q_{9_{(1,1)}} \mapsto \rm{False} ]
\end{align*}
変数の割り当ての中には、9 つの変数全てに False を割り当てたり複数個の変数に True を割り当てるものも存在するので、そのような割り当てを禁止する必要があります。
9 つの変数全てに False を割り当てる場合はこのセルに入る数字が 1 つもないのでルール 1 に反します。そこで、少なくとも 1 つの変数は True になるという論理式を Sat Solver に与える連言標準形に追加します。追加する論理式は以下の論理式です。
\begin{align*}
(q_{1_{(1,1)}} \lor q_{2_{(1,1)}} \lor q_{3_{(1,1)}} \lor q_{4_{(1,1)}} \lor q_{5_{(1,1)}} \lor q_{6_{(1,1)}} \lor q_{7_{(1,1)}} \lor q_{8_{(1,1)}} \lor q_{9_{(1,1)}})
\end{align*}
9 つの変数全てに False を割り当てるとこの論理式は False になります。すると Sat Solver は連言標準形で与えられた論理式を True にできないので、少なくとも 1 つの変数に True を割り当てます。
次に複数個の変数に True を割り当てることを禁止する論理式を追加します。
まず $q_{1_{(1,1)}}$ と $q_{2_{(1,1)}}$ で考えます。この 2 つの変数が同時に True になることを禁止するためには、2 つの変数に True が割り当てられた時にのみ False になる論理式を連言標準形に追加します。追加する論理式は以下の論理式です。
\begin{align*}
(\lnot q_{1_{(1,1)}} \lor \lnot q_{2_{(1,1)}})
\end{align*}
$q_{1_{(1,1)}}$ と $q_{2_{(1,1)}}$ が同時に True になることは禁止できたので、他の ${}_9 \mathrm{C} _2 - 1 = 35$ 通りの組み合わせについても論理式を追加します。
以上で、上の論理式と合わせて座標が (1, 1) のセルについてルール 1 の各セルには数字が 1 つ入るという条件を表現できました。
同様に残りの 80 個のセルについても変数と論理式を追加します。

次にルール 2 について考えます。
1 行目の数字の 1 に注目します。つまり、ルール 1 の場合と同様に 1 行目にあるセルの数字 1 に対応する 9 つの変数に注目します。
\begin{align*}
q_{1_{(1,1)}},\, q_{1_{(1,2)}},\, q_{1_{(1,3)}},\, q_{1_{(1,4)}},\, q_{1_{(1,5)}},\, q_{1_{(1,6)}},\, q_{1_{(1,7)}},\, q_{1_{(1,8)}},\, q_{1_{(1,9)}}
\end{align*}
1 行目に数字の 1 は少なくとも 1 つ入ります。また複数回出てきてはいけません。この条件はルール 1 について考えた場合と同じです。
そこで以下の論理式を追加します。
\begin{align*}
(q_{1_{(1,1)}} \lor q_{1_{(1,2)}} \lor q_{1_{(1,3)}} \lor q_{1_{(1,4)}} \lor q_{1_{(1,5)}} \lor q_{1_{(1,6)}} \lor q_{1_{(1,7)}} \lor q_{1_{(1,8)}} \lor q_{1_{(1,9)}})
\end{align*}
また、 ${}_9 \mathrm{C} _2$ 通りの組み合わせについて以下の論理式を追加します。
\begin{align*}
(\lnot q_{1_{(1,i)}} \lor \lnot q_{1_{(1,j)}})
\end{align*}
これで 1 行目の数字の 1 について、ちょうど 1 回入るという条件を表現できました。同様に、数字 2 から 9 についても追加します。同様に 2 行目から 9 行目についても条件を追加します。
以上でルール 2 を連言標準形に追加できました。

ルール 3 とルール 4 についてもルール 2 と同様に表現できます。
この状態で Sat Solver に可能な割り当てを求めさせると先に述べた 6,670,903,752,021,072,936,960 通りの配置のうちのどれかに対応する割り当てを返します。

ナンプレの問題を Sat Solver で解く

初期のヒントがすでに入っているナンプレの問題を Sat Solver で解くための手順を下の例を使って説明します。

問題例の座標が (1, 1) のセルを見ると数字の 6 が入っています。これは変数 $q_{6_{(1,1)}}$ に True が割り当てられている状態だと考えます。
Sat Solver に対して $q_{6_{(1,1)}}$ に必ず True を割り当てるように強制するためにはナンプレのルールを表現する連言標準形に変数をそのまま追加します。
\begin{align*}
(\text{ナンプレのルールを表現する論理式}) \land q_{6_{(1,1)}}
\end{align*}
$q_{6_{(1,1)}}$ に False を割り当てると Sat Solver は連言標準形で与えられた論理式を True にできないので、必ず $q_{6_{(1,1)}}$ に True を割り当てます。
同様に他のヒントについても対応する座標の対応する変数を連言標準形に追加していきます。
\begin{align*}
(\text{ナンプレのルールを表現する論理式}) \land q_{6_{(1,1)}} \land q_{5_{(1,2)}} \land q_{4_{(1,7)}} \land \dots \land q_{7_{(9,9)}}
\end{align*}
この論理式を True にする割り当てを Sat Solver が見つければ、それがこの問題の答えです。

答えが 1 つしかないことを Sat Solver で確認する

上の例題に対する論理式を True にする割り当てを探索すると下の答えが見つかります。

現状では、この数字の配置が初期のヒントと数独のルールを満たす答えの 1 つであるということしか確認できていません。これがただ 1 つの答えであることを確認する必要があります。そのために、問題を解いた時の論理式に見つけた答えに対応する割り当てを禁止する論理式を追加して再度 Sat Solver で問題を解きます。
追加する論理式は以下のようになります。
\begin{align*}
\lnot (q_{6_{(1, 1)}} \land q_{5_{(1,2)}} \land q_{9_{(1,3)}} \land \dots \land q_{3_{(9,8)}} \land q_{7_{(9,9)}})
\end{align*}
この論理式のままでは連言標準形の論理式に追加できないのでド・モルガンの法則を用いて以下のように変形します。
\begin{align*}
(\lnot q_{6_{(1, 1)}} \lor \lnot q_{5_{(1,2)}} \lor \lnot q_{9_{(1,3)}} \lor \dots \lor \lnot q_{3_{(9,8)}} \lor \lnot q_{7_{(9,9)}})
\end{align*}
この論理式は、見つけた答えに対応する割り当てと全く同じ割り当てをした場合にのみ False になります。Sat Solver に与える論理式は以下になります。
\begin{align*}
(\text{ナンプレのルールを表現する論理式}) \land (\text{ヒントに対応する論理式}) \land \\
(\lnot q_{6_{(1, 1)}} \lor \lnot q_{5_{(1,2)}} \lor \lnot q_{9_{(1,3)}} \lor \dots \lor \lnot q_{3_{(9,8)}} \lor \lnot q_{7_{(9,9)}})
\end{align*}
Sat Solver は論理式全体を True にするために先ほど見つけた割り当てとは違う割り当てを探索します。新たな割り当てが見つかれば答えが複数個存在することになるので、その問題は正当なナンプレの問題ではありません。新たな割り当てが見つからなければ正当な問題として採用します。

連言標準形への変換

Sat Solver は連言標準形の形の論理式しか受け付けてくれないので、解きたい問題を連言標準形の論理式に変換する必要があります。そこが難しいと感じた人も多いと思いますが、私はこの変換作業こそ面白いと感じます。ここでは変換の際に使えるテクニックを紹介します。
問題によっては、論理記号のならば $\Rightarrow$ を使って考えた方が考えやすい場合もあります。
\begin{align*}
X \Rightarrow Y
\end{align*}
は以下の論理式と同値なので変換は簡単にできます。
\begin{align*}
\lnot X \lor Y
\end{align*}
以下の論理式はどうでしょうか。
\begin{align*}
(X_{1} \wedge Y_{1})\vee (X_{2}\wedge Y_{2})\vee \dots \vee (X_{n}\wedge Y_{n})
\end{align*}
これを分配法則を用いて連言標準形の形に変換すると $2^{n}$ 個の節に変換されます。Sat Solver は非常に高速なのですが、節の数が多くなるとそれだけ計算に時間がかかるようになります。
実は、上の論理式を節の数が少ない論理的同値な論理式に変換する手法としてTseitin 変換という手法が知られています。
まずは、連言標準形の形にこだわらずに問題を論理式に変換した後でこれらの手法を用いて連言標準形に変換すると変換しやすくなります。

Sat Solver の応用例

ナンプレのルールは連言標準形に変換しやすい問題です。私はCalcBlocksを作成する際に以下のパズルも Sat Solver を用いて自動生成するプログラムを作成しています。
Sat Solver に習熟したい人はぜひこれらのパズルについても自動生成 + 答えの探索に挑戦してください。抽象的な問題を論理式に変換するとてもいい練習になります。

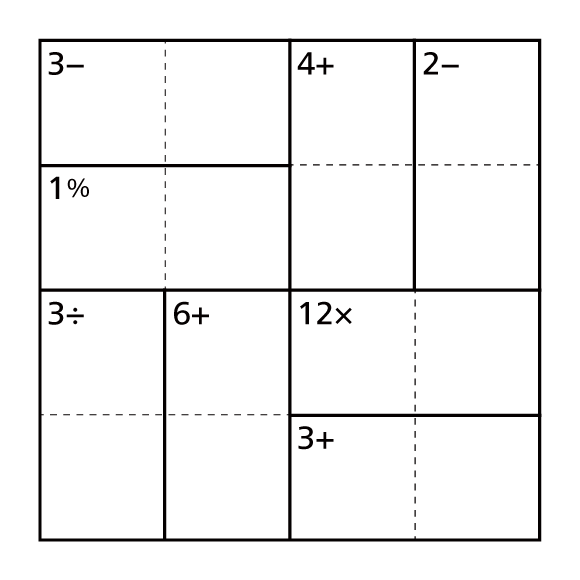
計算ブロック

各行、各列には 1 から 4 の各数字が1度ずつ入ります。
数字と演算子は各領域の和(＋)、大きい数と小さい数の差(－)、積(×)、大きい数を小さい数で割った商(÷)、大きい数を小さい数で割った余り(％) を表しています。
正解は 1 つだけです。

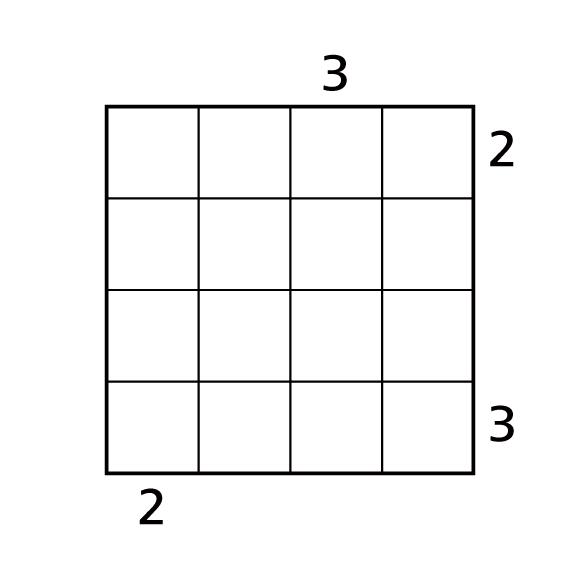
ビルディングパズル

高さが 1 から 4 のビルを上から見ています。
各行、各列にはビルの高さを表す 1 から 4 の各数字が1度ずつ入ります。
枠の外の数字はその方向から見えるビルの数を表しています。
正解は 1 つだけです。

ナンバーリンク

同じ数字どうしを 1 本の線でつなぎます。
それぞれの線は枝分かれしたり、交わったりしてはいけません。
それぞれのマスを通過する線は 1 本だけです。また空白のマスはありません。
正解は1つだけです。

スリザーリンク

点と点を線でつなぎ、全体で 1 つの閉じた輪をつくります。
４つの点で作られた正方形の中にある数字は、その正方形の辺に引く線の数を表しています。数字のない正方形には何本の線を引くかわかりません。
線を交差させたり、枝分かれさせたりしてはいけません。
正解は 1 つだけです。

対称性を用いた問題の複製

ナンプレの問題を 1 つ見つけた後で Sat Solver のように計算のコストが高い処理をせずに別のナンプレの問題を作ることは可能でしょうか？
ヒントの数字を好き勝手移動すると正解のない問題や正解が複数ある問題になる可能性があります。するともう一度 Sat Solver で確認する必要があります。一方で次の例のように、ヒントの数字全体を同時に 90 度回転した問題は、正解も 90 度回転したものになるので正当なナンプレの問題になります。

90 度の回転のように特定の規則に従ってヒントの数字を移動してできた問題は、再度チェックしなくても新しい問題として使えそうです。ではこのような移動にはどのようなものがいくつあるでしょうか？

わかりやすくするために 4 つの角に数字を振った正方形を考えます。この 4 つの数字を何らかの対称性に従って移動する方法には以下の方法があります。

それぞれの対称性に従った移動を次のように名付けます。

点対称による移動は $\delta$ 変換
線対称による上下移動は $\alpha$ 変換
線対称よる右上と左下の数字の移動を $\beta$ 変換
回転対称にる 90 度の回転移動を $\gamma$ 変換

図では 1 度の移動しか行なっていませんが続けて複数回の移動をする場合も考えます。この時、初めの配置から複数回の変換を行うことでたどり着くことができる数字の配置をすべて求めます。これは数学的には以下のように表現されます。

$\alpha,\beta,\gamma,\delta$ 変換によって生成される群の位数を求めよ

それぞれの変換の間には以下の等式が成り立ちます。変換を全く行わない場合を恒等変換と呼び $\bf{Id}$ で表します。
\begin{align*}
\alpha^{2} &= \bf{Id} \\
\beta^{2} &= \bf{Id} \\
\gamma^{4} &= \bf{Id} \\
\delta^{2} &= \bf{Id} \\
\gamma^{2} &= \delta \\
\alpha \beta &= \gamma \\
\beta \alpha &= \gamma^{3} \\
\alpha \gamma &= \beta \\
\gamma \alpha &= \gamma^{2} \beta = \beta \gamma^{2} \\
\beta \gamma &= \alpha \gamma^{2} = \gamma^{2} \alpha \\
\gamma \beta &= \alpha
\end{align*}

この等式を用いて全ての変換を $\alpha$ 変換と $\beta$ 変換だけで表すと以下の 8 つになります。
$\{ \bf{Id}, \alpha, \beta, \alpha \beta, \beta \alpha, \alpha \beta \alpha, \beta \alpha \beta, \alpha \beta \alpha \beta \}$
それそれの変換に対応する数字の位置は以下の通りです。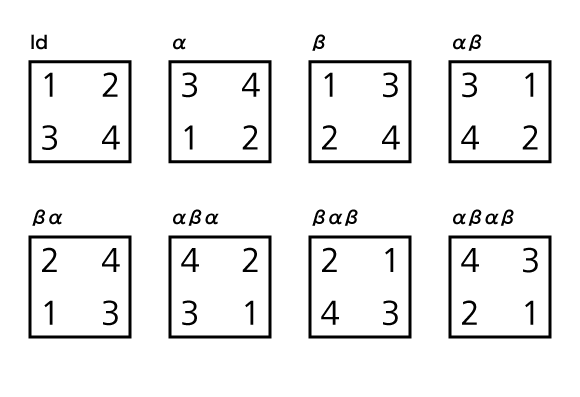

結論として、1 つナンプレの問題が見つかるとその問題から追加で 7 つの問題を変換のコストだけで作成できます。
ただし、元の問題が正当なナンプレの問題であるときに、 $\alpha$ 変換等を適用した後の問題も正当なナンプレの問題になっていることを証明しないといけません。正当なナンプレの問題が満たすべき論理式を正確に定義した上で証明をしてみてください。