Steve Awodey の Category Theory を読む シリーズトップ
- 9.1 Preliminary definition
- 9.2 Hom-set definition
- 9.4 Order adjoints
- 9.5 Quantifiers as adjoints
- 9.6 RAPL
- 9.7 Locally cartesian closed categories
- 9.8 Adjoint functor theorem
- 参考書籍
9.1 Preliminary definition
Example 9.3
を
で定義した時、
が forgetful functor
の left adjoint となることを証明します。はじめに
の定義が well-defined であることを証明します。
任意の に対して
が cocomplete poset となることを示せばよい。
に
を順序として入れると poset になることは明らかであるから、
が cocomplete になることを示す。
任意の index set に対して
となることを示せばよい。任意の
と任意の
に対して
より
が成り立つ。
であるから、
の定義より
が成り立つ。よって
が成り立つので
が成り立つ。
次に、任意の に対して
を定義する必要があります。その前に、任意の
に対して
を
と定義するとき、次のことが成り立つことを証明します。
任意の に対して
であるから
が成り立つ。
逆に とすると
が成り立つので
が成り立つ。すると
であることから
が成り立つ。
上の事実をもとに、任意の と任意の
に対して
を
で定義します。このとき
が well-defined であることを証明します。
任意の と任意の
に対して
となることを示せばよい。
任意の と任意の
に対して、
が成り立つから、
なら
となり
が成り立つ。よって
である。
このとき、証明は省略しますが は functor の条件 (a), (b), (c) を満たすので functor となります。
次に が forgetful functor
の left adjoint となることを証明します。はじめに、任意の
に対して
を任意の
に対して
で定義します。このとき
が monotone かつ cocontinuous であることを証明します。
- monotone であること
任意の に対して
を示せばよい。任意の
に対して
であるから、
が成り立つので colimit の UMP より
が成り立つ。
- cocontinuous であること
任意の index set に対して
が成り立つことを示せばよい。定義よりこれは
と同値である。
任意の に対して
が成り立つので、colimit の UMP より
が成り立つ。
一方、任意の と任意の
に対して
が成り立つので、colimit の UMP より
が成り立つ。
次に を
で定義します。このとき
が natural transformation になることを証明します。
任意の に対して以下の diagram が可換になることを示せばよい。
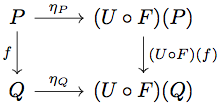
これは任意の に対して
が成り立つことと同値である。
- only if case
とすると、
が成り立つ。すると
であるから
となる。
- if case
とすると、ある
が存在して
が成り立つ。
は monotone であるから
が成り立つので、
が成り立つ。
任意の に対して
となることを示せばよい。
より
となることは明らかである。逆に、任意の
とすると
であり、
が monotone であるから
が成り立つ。よって colimit の UMP より
が成り立つ。
最後に の唯一性について証明する。
任意の に対して
が成り立つことと
が cocontinuous であることに注意すると、
\begin{align*}
g(U) &= g\left( \bigcup_{p \in U} p\!\downarrow \right) \\
&= \bigvee_{p \in U} g(p\!\downarrow) \\
&= \bigvee_{p \in U} f(p) \\
&= \overline{f}(U)
\end{align*}
が成り立つ。
9.2 Hom-set definition
で定義された
が natural transformation であることを証明します。
任意の に対して以下の diagram が可換になることを示せばよい。
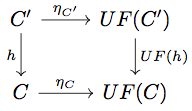
が natural であることから以下の diagram が可換になることに注意すると、
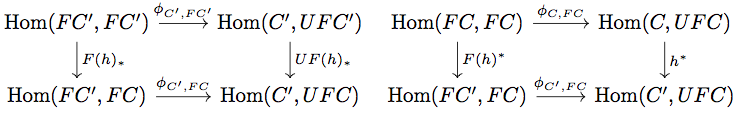
\begin{align*}
UF(h) \circ \eta_{C'} &= UF(h) \circ \phi_{C', FC'}(1_{FC'}) \\
&= \left( UF(h)_{\ast} \circ \phi_{C', FC'} \right)(1_{FC'}) \\
&= \left( \phi_{C', FC} \circ F(h)_{\ast} \right)(1_{FC'}) \\
&= \phi_{C', FC}\left( F(h) \right) \\
&= \phi_{C', FC} \left( 1_{FC} \circ F(h) \right) \\
&= \left( \phi_{C', FC} \circ F(h)^{\ast} \right)(1_{FC}) \\
&= \left( h^{\ast} \circ \phi_{C, FC} \right)(1_{FC}) \\
&= \phi_{C, FC}(1_{FC}) \circ h \\
&= \eta_{C} \circ h
\end{align*}
が成り立つ。
9.4 Order adjoints
この節で出てくる例は、adjoint functor の domain も codomain も Preorder set を圏と見なしたものなので、任意の対象間には高々一つの写像しか存在しません。
よって同型射が natural になることは自明に成り立つのでその証明は省略されています。
Example 9.12
こちらの記事でも言及したのですが、ここの記述は正確ではありません。ただし位相空間に詳しくない方は飛ばして構いません。
書籍にあるように dual image function を と定義した場合、
は確かに
の right adjoint になります。これは、
かつ
が成り立つことを確認すればいいです。
問題はその次で、 を開集合に制限して
とした場合にも
が
の right adjoint になるという記述です。というのも
を任意の
の開集合とした時に
は必ずしも
の開集合とはならないからです。よって
は
の right adjoint にはなり得ません。
そこで という書籍を参照すると、そこでは dual image function を以下のように定義しています。
この定義を用いると、任意の の開集合
に対して
は
の開集合になり
の right adjoint になることが証明できます。一方で開集合に制限しない
に対しては right adjoint になりません。
以上の二つの定義とその結果が、ここの記述ではごちゃ混ぜになっています。上で述べたことを是非自分で確認してみてください。
9.5 Quantifiers as adjoints
Figure 9.1 の説明がわかりにくいかもしれないので補足しておきます。ちなみに Figure 9.1 にある は
の誤りです。
Figure 9.1 の左下を原点として、水平方向を 軸、垂直方向を
軸とします。また
上の任意の領域
に対して
によって生成される長方形をそのまま
と書くことにします。さらに斜線で塗られた領域を、領域
と呼ぶことにします。
- 上から下に読む場合
を満たす
軸上の領域
が
を満たす
軸上の領域、つまり Figure 9.1 の
と書かれた領域を含むのであれば、
は領域
を含むと読みます。
- 下から上に読む場合
を満たす
軸上の領域
に対して
が領域
を含むのであれば、
は
を含むと読みます。
同様に
- 上から下に読む場合
を満たす
軸上の領域
に対して
が領域
に含まれるならば、
は
に含まれると読みます。
- 下から上に読む場合
を満たす
軸上の領域
が
に含まれるのであれば、
は領域
に含まれると読みます。
9.6 RAPL
Proposition 9.16
ここでは の定義と
が functor になることの証明、
の定義と
が functor になることの証明が省略されています。
さらに natural isomorphism であることを示すところで、isomorphism であることは示されていますが、natural であることの証明が省略されています。 に関して natural になることは Chapter 8 で確認しましたが
に関して natural になることは確認していないので、ここで確認しておきます。
の定義
任意の natural transformation に対して次の diagram を考える。
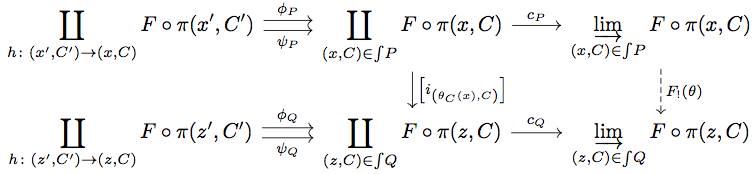
ここで任意の に対して
、
である。
は
の合成である。
また が natural であるから
が成り立つことから
は
となることに注意する。すると
\begin{align*}
c_{Q} \circ \left[ i_{\left( \theta_{C}(x), C \right)} \right] \circ \phi_{P} \circ i_{h} &= c_{Q} \circ i_{\left( \theta_{C'}(x'), C' \right)} \\
&= c_{Q} \circ \phi_{Q} \circ i_{h} \\
&= c_{Q} \circ \psi_{Q} \circ i_{h} \\
&= c_{Q} \circ i_{\left( \theta_{C}(x), C \right)} \circ F(h) \\
&= c_{Q} \circ \left[ i_{\left( \theta_{C}(x), C \right)} \right] \circ \psi_{P} \circ i_{h}
\end{align*}
が成り立つ。よって coproduct の UMP と colimit の UMP より diagram を可換にする写像 がただ一つ存在する。これを
と定義する。
が functor であること
となるから
は functor の条件 (a) を満たす。
は上の diagram の
を
で置き換えると、colimit の UMP より
が成り立つことがわかる。よって
は functor の条件 (b) を満たす。
は
が成り立つので colimit の UMP より
が成り立つ。よって
は functor の条件 (c) を満たす。
次に が functor であることを証明します。
- 任意の
に対して
が functor であること
任意の に対して
を
で定義する。
となるので
は functor の条件 (a) を満たす。
が成り立つので
は functor の条件 (b) を満たす。
が成り立つ。よって
は functor の条件 (c) を満たす。
が functor であること
任意の に対して
を任意の
に対して
で定義する。
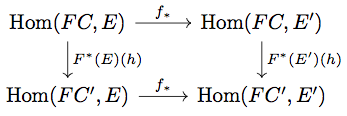
任意の と任意の
に対して
が成り立つので、上の diagram は可換になる。よって
は natural transformation である。
このとき が成り立つので
は functor の条件 (a) を満たす。
は定義より明らか。よって
は functor の条件 (b) を満たす。
が成り立つので、
は functor の条件 (c) を満たす。
最後に が
に関して natural であることを証明します。
の場合は
の場合と同様に示せるので、
が natural であることの証明のみを示します。それ以外の箇所は Chapter 8 で示した証明と同様に証明できるので省略します。
の定義は Chapter8 の 8.7 節の証明を参照してください。
任意の について考える。
が natural であるためには以下の diagram が可換になることを示す必要がある。
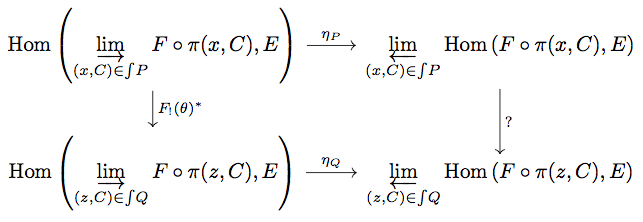
しかし diagram の右の写像がどのような写像なのか明らかではない。そこで以下の diagram を考える。
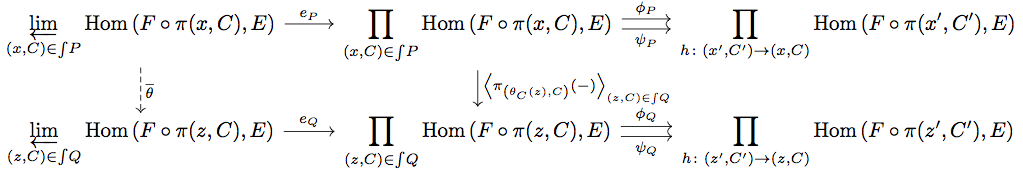
ここで が natural であることから、任意の
は
となることに注意しておく。すると
\begin{align*}
\pi_{h} \circ \phi_{Q} \circ \left< \pi_{\left( \theta_{C}(z), C \right)}(-) \right>_{(z,C) \in \int\!Q} \circ e_{P} &= \pi_{(z',C')} \circ \left< \pi_{\left( \theta_{C}(z), C \right)}(-) \right>_{(z,C) \in \int\!Q} \circ e_{P} \\
&= \pi_{\left( \theta_{C'}(z'), C' \right)} \circ e_{P} \\
&= \pi_{h} \circ \phi_{P} \circ e_{P} \\
&= \pi_{h} \circ \psi_{P} \circ e_{P} \\
&= F(h)^{\ast} \circ \pi_{\left( \theta_{C}(z), C \right)} \circ e_{P} \\
&= F(h)^{\ast} \circ \pi_{(z,C)} \circ \left< \pi_{\left( \theta_{C}(z), C \right)}(-) \right>_{(z,C) \in \int\!Q} \circ e_{P} \\
&= \pi_{h} \circ \psi_{Q} \circ \left< \pi_{\left( \theta_{C}(z), C \right)}(-) \right>_{(z,C) \in \int\!Q} \circ e_{P}
\end{align*}
が成り立つので、product の UMP と limit の UMP より diagram を可換とする唯一つの が存在する。
次に を示す。すると product の UMP と
が monic であることから
が成り立つ。
任意の に対して
\begin{align*}
\left( \pi_{(z,C)} \circ e_{Q} \circ \overline{\theta} \circ \eta_{P} \right)(f) &= \left( \pi_{\left( \theta_{C}(z), C \right)} \circ e_{P} \circ \eta_{P} \right)(f) \\
&= \left( \pi_{\left( \theta_{C}(z), C \right)} \circ \left< - \circ i_{(x,C)} \right>_{(x,C) \in \int\!P} \circ c_{P}^{\ast} \right)(f) \\
&= f \circ c_{P} \circ i_{\left( \theta_{C}(z), C \right)} \\
&= f \circ c_{P} \circ \left[ i_{\left( \theta_{C}(z), C \right)} \right] \circ i_{(z,C)}
\end{align*}
が成り立つ。一方、
\begin{align*}
\left( \pi_{(z,C)} \circ e_{Q} \circ \eta_{Q} \circ F_{!}(\theta)^{\ast} \right)(f) &= \left( \pi_{(z,C)} \circ \left< - \circ i_{(z,C)} \right>_{(z,C) \in \int\!Q} \circ c_{Q}^{\ast} \circ F_{!}(\theta)^{\ast} \right)(f) \\
&= f \circ F_{!}(\theta) \circ c_{Q} \circ i_{(z,C)}
\end{align*}
が成り立つ。これは の定義より等しい。よって
は natural isomorphism である。
最後にこのように定義した に対して
が成り立つことを証明します。
において
は terminal object になるので、任意の
に対して
が存在する。このことに注意すると、任意の natural transformation
に対して次の左の diagram は可換となる。
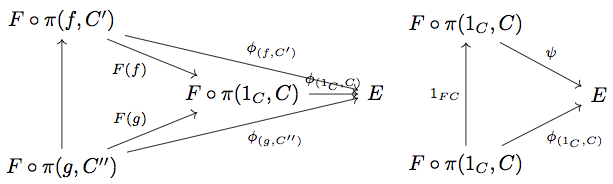
また任意の が存在して同様に diagram を可換にするとすると、上の右の diagram が可換になることより
が成り立つ。
よって colimit の UMP より が成り立つ。
9.7 Locally cartesian closed categories
Proposition 9.20
はじめに、任意の に対して
が成り立つとき、
が成り立つことを確認してください。
の二つの natural isomorphism を合成すればいいです。
次に に対して
が
となることは Proposition 5.14 で確認しました。すると
の right adjoint は
に unique up to isomorphism で決まるので、
で定義すればよいことがわかります。
次に証明なしに出てくる "a slice of a slice is a slice" の確認をしておきます。
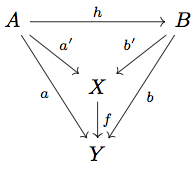
任意の と任意の
について
となることを示す。
はじめに functor を定義する。
任意の に対して
と定義すると、
であるから
となる。
また任意の に対して
と定義すると、
は
を満たすので
となる。
このとき、 が成り立つので、
は functor の条件 (a) を満たす。
次に が成り立つので
は functor の条件 (b) を満たす。
最後に が成り立つので
は functor の条件 (c) を満たす。
次に functor を定義する。
任意の に対して
を
で定義する。明らかに
である。
また任意の に対して
と定義すると、
は
を満たすので、
となり functor の条件 (a) を満たす。
次に が成り立つので
は functor の条件 (b) を満たす。
最後に が成り立つので
は functor の条件 (c) を満たす。
以上のように定義した 、
に対して
かつ
が成り立つことは明らかであるから、
が成り立つ。
任意の に対して composition functor
を考えます。
上の同型射を用いると が構成できます。
が locally cartesian category なら、
に対して right adjoint
、
が構成できます。よって再び同型射を用いることで
に対して right adjoint を構成できるので
も locally cartesian category になります。
逆の の証明は exponential が突然出てきて難しいですね。
を使った置き換えがなぜ必要なのかもよくわかりません。また1対1に対応するとは書かれていますが、それが
と
に対して natural であることの証明は省略されています。
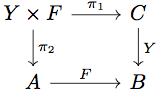
任意の の composition functor の right adjoint
は pullback functor である。よって上の図のように任意の
に対して
となる。
、
は
における射であるから
を
の object のように記述するのはおかしいが、
においては
は確かに
となるのでこのように記述している。このとき
、
は実際に
において projection function になっている。
以上の注意を元に、任意の と
に対して
を定義する。
任意の に対して以下の diagram を考える。
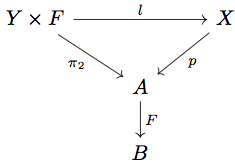
は
と考えると
と見なせる。
は cartesian closed であるので exponential の UMP より
が存在する。
が
と見なせることに注意して以下の pullback diagram in
を考える。
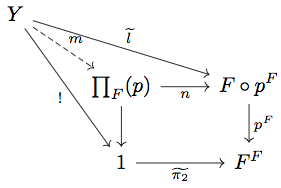
すると、 が成り立つ。一方、
が成り立つので exponential の UMP より
が成り立つ。よって pullback の UMP より
が存在する。そこで
で定義する。これは各 UMP により well-defined である。
次に を定義する。
任意の に対して、上の diagram において
を考える。すると exponential の UMP より
が存在する。この
を
とみなして、
で定義する。
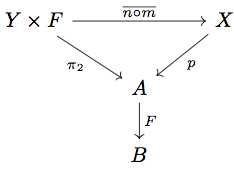
は
の逆射になるので、
は isomorphism である。次に natural であることを示す。
が
に関して natural であること
任意の に対して Two-pullback Lemma より以下の diagram が可換になる。
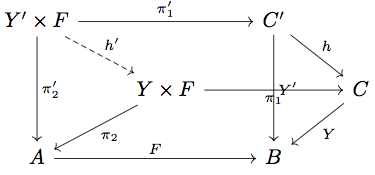
すると は
とみなすことができる。そこで次の左の diagram を考える。
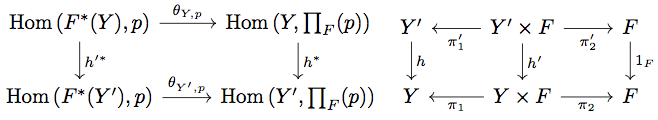
任意の に対して、
が成り立つ。一方、
が成り立つ。
に対して
の定義より、
が成り立つ。同様に
に対して
が成り立つ。
Two-pullback Lemma による diagram より上の右の diagram は可換になる。よって が成り立つので、exponential の UMP と pullback の UMP より
が成り立つ。
が
に関して natural であること
任意の に対して Two-pullback Lemma より以下の diagram が可換になる。
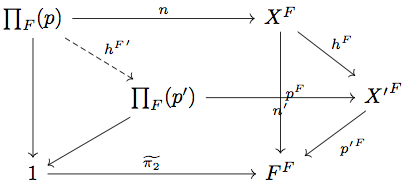
そこで次の diagram を考える。
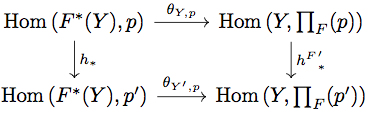
任意の に対して、
が成り立つ。一方、
が成り立つ。
上の Two-pullback Lemma による diagram と の定義より
\begin{align*}
\epsilon \circ \left( n' \circ {h^{F}}' \circ \theta_{Y,p}(l) \times 1 \right) &= \epsilon \circ \left( h^{F} \circ n \circ \theta_{Y,p}(l) \times 1 \right) \\
&= h \circ \epsilon \circ \left( n \circ \theta_{Y,p}(l) \times 1 \right) \\
&= h \circ l
\end{align*}
が成り立つ。一方、 が成り立つ。よって exponential の UMP と pullback の UMP より
が成り立つ。
以上より は natural isomorphism である。
Lemma 9.23
ここでは を定義し、
かつ
を示す必要があります。
はじめに を定義するために、任意の
に対して functor
を定義します。
任意の に対して1つ目の成分が
であるような
の object の集合を
と表す。このとき
で定義する。
次に任意の に対して、
は任意の
に対して
となる。すると
は
となることに注意して、
で定義する。
このとき が functor の条件をみたすことは coproduct の UMP により明らかである。
本当に が functor の条件を満たすか確認してください。
次にこの を用いて
を
で定義する。このとき
が functor となることを示す。
任意の と任意の
に対して
の要素を
で表すとすると、
を
で定義する。このとき
が natural transformation であることを示す。
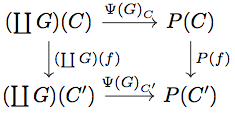
任意の と任意の
に対して
が成り立つ。一方米田の補題より
\begin{align*}
\left( \Psi(G)_{C'} \circ (\coprod G)(f) \right)( (C,x), l) &= \Psi(G)_{C'}\left( (C', x \circ yf), G(yf)(l) \right) \\
&= (x \circ yf)_{C}(1_{C}) \\
&= P(f)(x_{C}(1_{C}))
\end{align*}
が成り立つので、上の diagram は可換となり となる。
次に、任意の に対して
を
で定義する。このとき
が natural であることを示す。

任意の と任意の
に対して
一方
が成り立つ。これらは が natural であることより等しい。上の左の diagram は可換であるので
は natural である。
また任意の に対して
が成り立つので、 となる。
が functor の条件をみたすことは coproduct の UMP 等により明らかである。
natural isomorphism を構成すればよい。
任意の と任意の
に対して
となることに注意して、
を任意の
に対して
で定義する。ただし
は米田の補題により一意に定まる
を満たす natural transformation とする。
任意の に対して
で
を定義すれば、明らかに
は isomorphism となる。
が
に関して natural であることを示す。
任意の に対して以下の diagram を考える。
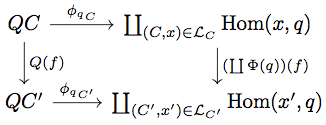
任意の に対して
が成り立つ。一方、 が成り立つ。
が成り立つので両者は等しい。よって diagram は可換となる。
この に対して以下の diagram が可換になることは明らかなので、
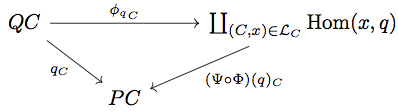
となる。
最後に任意の に対して以下の diagram を考える。
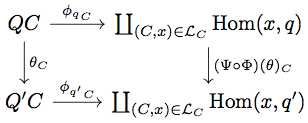
任意の に対して
が成り立つ。一方、 が成り立つ。
ところが が成り立つので、両者は等しい。よって上の diagram は可換となる。
以上より は natural isomorphism である。
natural isomorphism を構成すればよい。
任意の と任意の
に対して
を次のように定義する。
任意の に対して
は
つまり
であるから米田の補題より一意に対応した
が得られる。
この に対して以下の diagram を考える。

任意の に対して米田の補題と
の定義より、
\begin{align*}
\left( \Psi(G)_{C'} \circ \widetilde{l}_{C'} \right)(f) &= \Psi(G)_{C'}( (C', x \circ yf), G(yf)(l)) \\
&= (x \circ yf)_{C'}(1_{C'}) \\
&= P(f) \left( x_{C'}(1_{C'}) \right) \\
&= x_{C'}(f)
\end{align*}
が成り立つので、上の diagram は可換になる。よって となるので
と定義する。
次に が isomorphism であることを示す。
を次のように定義する。
任意の に対して、
は
と見なせるので米田の補題より
が一意に存在して
を満たす。このとき
が
をみたすことから
が成り立つ。よって
である。
そこで と定義すると、米田の補題より
の逆射となり
は isomorphism となる。
次に が natural であることを示す。
任意の に対して次の diagram を考える。
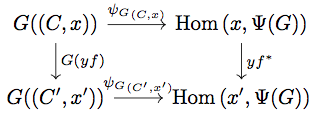
任意の に対して
が成り立つ。一方
が成り立つ。
今、、
が成り立ち両者は等しいので、米田の補題より diagram は可換となる。よって
は natural である。
最後に が natural であることを示す。
任意の と任意の
に対して次の diagram を考える。
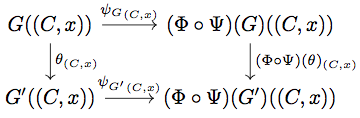
任意の に対して
が成り立つ。一方
が成り立つ。
今 、
が成り立つので、米田の補題より上の diagram は可換となる。
以上より は natural isomorphism である。
9.8 Adjoint functor theorem
Theorem 9.29
書籍にある Solution set condition が微妙に間違ってます。書籍にある通り論理式で表現すると
となりますが、正しくは
となります。
こちらの条件でないと、Theorem 9.29 の証明の中で Lemma 9.30 を使用することができません。
参考書籍

Category Theory (Oxford Logic Guides)
- 作者:Awodey, Steve
- 発売日: 2008/01/10
- メディア: ペーパーバック

- 作者:スティーブ アウディ
- 発売日: 2015/09/19
- メディア: 単行本