Steve Awodey の Category Theory を読む : Chapter 3

Steve Awodey の Category Theory を読む シリーズトップ

3.2 Coproducts

Example 3.5

を の UMP より を満たすただ一つの arrow とする。同様に を定める。このとき、 が 、 の coproduct となることを示す。
任意の と任意の に対して、 と を考えると、 の UMP より が存在する。すると の UMP より が存在して、 を満たす。この に対して、

\begin{align*}
\left| [f,g] \circ i_{M(A)} \right| \circ \eta_{A} &= \left| [f,g] \right| \circ \left| i_{M(A)} \right| \circ \eta_{A} \\
&= \left| [f,g] \right| \circ \eta_{A+B} \circ i_{A} \\
&= [\left| f \right| \circ \eta_{A}, \left| g \right| \circ \eta_{B}] \circ i_{A} \\
&= \left| f \right| \circ \eta_{A}
\end{align*}

が成り立つので、 の UMP より が成り立つ。同様に が成り立つので、 は diagram を可換にする。
次に、任意の が diagram を可換にするとする。すると

\begin{align*}
\left| h \right| \circ \eta_{A+B} \circ i_{A} &= \left| h \right| \circ \left| i_{M(A)} \right| \circ \eta_{A} \\
&= \left| h \circ i_{M(A)} \right| \circ \eta_{A} \\
&= \left| f \right| \circ \eta_{A}
\end{align*}

が成り立つ。同様に が成り立つので、 の UMP より、 である。よって の UMP より が成り立つので、 は 、 の coproduct である。

free monoid の UMP や、coproduct の UMP を適宜使用する必要があってちゃんと証明しようとすると複雑ですね。coproduct の UMP を証明するために、diagram を可換にする arrow が存在することと、それがただ一つに決まることの2つを証明していることを確認してください。

Example 3.6

一般に 、 が位相空間のとき、 の位相は で定義されます。

任意の と任意の に対して、 を Example 3.4 と同様に定義すると、可換性と唯一性は Example 3.4 で証明済みなので が continuous であることを示せばよい。
任意の に対して、 であるが、、 が continuous であることより、、 が成り立つ。 の定義より となるから、 は continuous である。

Example 3.9

この Example の証明は非形式的な証明でさらっと流されていますが、形式的に証明しようとすると結構大変です。
書籍では、binary relation は4つの等式を含んだ最小の equivalence relation であるとだけ書かれていますが、具体的にどのように構成するのか書かれていません。4つの等式を 上の二項関係と表現したときに生成される最小の equivalence relation の構成については下の記事に書いたのでそちらを参照してください。
www.orecoli.com

、 が homomorphism となることは明らかなので省略します。 と が において一致して、かつ の単位元になる必要があるので、4つの等式の上の二つを含む equivalence relation で割る必要があるということを確認してください。
ここでは、書籍にあるように で定義される が well-defined であることを証明します。

\begin{equation}
\forall [v], [w] \in M(\left| A \right| + \left| B \right|)\, / \sim,\, [v] = [w] \Rightarrow [f,g]([v]) = [f,g]([w])
\end{equation}

4つの等式を表現する 上の二項関係を とする。
先に参照した記事の内容より、 が成り立つ。よって が存在して、、 かつ が成り立つ。 に関する帰納法により示す。

• のとき

の場合は明らか。 のとき、 を 上の任意の word とすると、 の場合を考える。このとき、

\begin{align*}
[f,g]'(su_{A}s') &= [f,g]'(s) \cdot f(u_{A}) \cdot [f,g]'(s') \\
&= [f,g]'(s) \cdot u_{M} \cdot [f,g]'(s') \\
&= [f,g]'(s) \cdot [f,g]'(s') \\
&= [f,g]'(ss')
\end{align*}

が成り立つので、 が成り立つ。 の場合も同様である。
のとき、

\begin{align*}
[f,g]'(saa's') &= [f,g]'(s) \cdot f(a) \cdot f(a') \cdot [f,g]'(s') \\
&= [f,g]'(s) \cdot f(a \cdot_{A} a') \cdot [f,g]'(s') \\
&= [f,g]'(s) \cdot [f,g]'(a \cdot_{A} a') \cdot [f,g]'(s') \\
&= [f,g]'(s(a \cdot_{A} a')s')
\end{align*}

が成り立つので、 が成り立つ。 の場合も同様である。
の場合も同様に成り立つ。

• のとき

帰納法の仮定より、 が成り立つ。また の場合と同様の議論により、 が成り立つ。よって が成り立つ。

が homomorphism であることは が homomorphism であることから明らかです。
また を自然な homomorphism とすると、 が成り立ちます。任意の が を満たすなら が成り立つことも簡単に確かめられます。
最後に が 、 を満たすただ一つの arrow であることを証明します。

\begin{equation}
\forall h \colon M(\left| A \right| + \left| B \right|)\, / \sim \to M,\, h \circ i_{A} = f \land h \circ i_{B} = g \Rightarrow h = [f,g]
\end{equation}

を示せばよい。それには の UMP より、 を示せばよい。それには の UMP より、 かつ を示せばよい。
任意の に対して、

\begin{align*}
(\left| h \circ \pi \right| \circ \eta_{\left| A \right| + \left| B \right|} \circ i_{\left| A \right|})(a) &= h([a]) \\
&= \left| h \circ i_{A} \right| (a) \\
&= \left| f \right| (a)
\end{align*}

が成り立つ。同様に、 が成り立つので が成り立つ。

Example 3.10

任意の と任意の に対して、 を で定義する。すると が成り立つ。同様に が成り立つので、 は diagram を可換にする。
一方、任意の が diagram を可換にするとすると、任意の に対して、 が成り立つ。よって は 、 の coproduct である。

Proposition 3.11

証明の中で zero homomorphism という言葉が出てきます。 においては は initial object かつ terminal object となり、そのような対象を zero object と呼びます。
この zero object を用いると、任意の対象 間に なる arrow が存在することがわかります。( の箇所では が terminal object であることを利用し、 の箇所では が initial object であることを利用しています。)

3.4 Coequalizers

Example 3.20

集合圏 において任意の に対して coequalizer を具体的に構成します。
を で定義される 上の二項関係とし、 を から生成される equivalence relation とします。このとき、 を任意の に対して で定義します。

任意の に対して、、 であるから、 つまり を示せばよい。これは の定義より、、、 とすれば、 であるから が成り立つ。

次に任意の が を満たすとき、 を で定義します。このとき、 が well-defined であることを証明します。

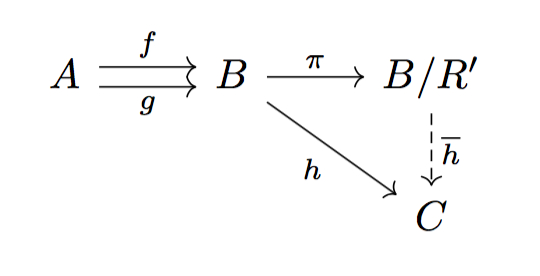
\begin{equation}
\forall b,b' \in B,\, [b] = [b'] \Rightarrow \overline{h}([b]) = \overline{h}([b'])
\end{equation}

であるから である。よって が存在して、、 かつ が成り立つ。 に関する帰納法により示す。

• のとき

なら は明らかである。
なら が存在して、 かつ であるから、 が成り立つ。
なら が存在して、 かつ であるから、 が成り立つ。

• のとき

帰納法の仮定より が成り立つ。 に対して、 の場合と同様の議論により が成り立つ。よって が成り立つ。

が成り立つことは定義より明らかです。また が epic であるから、 はただ一つに決まります。よって は の coequalizer になります。

参考書籍

Category Theory (Oxford Logic Guides)

圏論 原著第2版