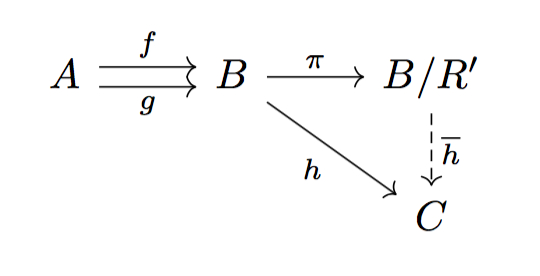Errata list for An Introduction to Algebraic Topology 4th edition.

数学

はじめに

私は数年前に Joseph J Rotman著 『An Introduction to Algebraic Topology』を読んで、代数的トポロジーの勉強をしました。当時日本語で書かれた代数的トポロジーの書籍を何冊か探したのですが、定義や証明が十分に形式的に記述されているものはありませんでした。この本は、非常に定義、証明共に厳密で自習するには最適だったのですが、とにかく誤植が多い印象を受けました。
私が見つけた誤植を全て tex ファイルにして著者に送付したのですが何の response も得られませんでした。そこで、放置するのももったい無いので私のブログで公開しておきます。
これからこの書籍を使って勉強する人の役に少しでも立てばと思います。(詳細はすっかり忘れているので、質問には答えられないと思います)

Errata list

page 53 line 5

\pi_{1}(R^{1},1) to \pi_{1}(S^{1},1)

page 74 line -3

\displaystyle \sum{m_{i}\partial(b.\sigma_{i})} = \sum{m_{i}(b-x_{i})} = (\sum{m_{i}})b-\gamma
to
\displaystyle \sum{m_{i}\partial(b.\sigma_{i})} = \sum{m_{i}(x_{i}-b)} = \gamma-(\sum{m_{i}})b

\sum{m_{i}\partial(b.\sigma_{i})} equals to \sum{m_{i}( (b.\sigma_{i})(e_{1}) - (b.\sigma_{i})(e_{0}))}, and
applying e_{1}(or e_{0}) to b.\sigma means that applying t=0(or t=1) to the equation (b.\sigma)(t) = tb + (1-t)x.

page 77 line -7

(\lambda^{X}_{1} - \lambda^{X}_{0} - P^{X}_{n-1}\partial_{n})(\sigma)
to
({\lambda^{X}_{1}}_{\#} - {\lambda^{X}_{0}}_{\#} - P^{X}_{n-1}\partial_{n})(\sigma)

page 114 line 6

I think that the sentence "It is easy to see that both definitions of \text{Sd}_{n}(\sigma) agree when X is convex."
should be deleted or be changed to
"It is easy to see that both definitions of \text{Sd}_{n}(\sigma) agree when X is convex and \sigma is affine."
(when \sigma is called \textit{affine} will be defined in latter page!)

According to the definition of barycentric subdivision when X is a convex set,
\[\text{Sd}_{n}(\sigma) = \sigma(b_{n}).\text{Sd}_{n-1}(\partial\sigma) =
\begin{cases}
\sigma(b_{n}) & \text{if}\ t_{0} = 1 \\
t_{0}\sigma(b_{n}) + (1 - t_{0})\text{Sd}_{n-1}(\partial\sigma) \left( \frac{t_{1}}{1-t_{0}}, \dots ,\frac{t_{n+1}}{1-t_{0}} \right) & \text{if}\ t_{0} \neq 1
\end{cases} \].

On the other hand, according to the definition of barycentric subdivision when X is any space,
\[\text{Sd}_{n}(\sigma) = \sigma_{\#}\text{Sd}_{n}(\delta^{n}) =
\begin{cases}
\sigma(b_{n}) & \text{if}\ t_{0} = 1 \\
\sigma \left( t_{0}b_{n} + (1 - t_{0})\text{Sd}_{n-1}(\partial\delta^{n}) \left( \frac{t_{1}}{1-t_{0}}, \dots ,\frac{t_{n+1}}{1-t_{0}} \right) \right) & \text{if}\ t_{0} \neq 1
\end{cases}\].
These two do not coincide if \sigma is not \textit{affine}.

page 118 line -4

D = d h_{\#}^{-1} q_{\#}
to
D = d h_{*}^{-1} q_{*}

page 157 line 14

"the first is 18 \times 27 and the second is 27 \times 9"
to
"the first is 27 \times 18 and the second is 9 \times 27"

page 159 line -12

z - z' \in B_{q}
to
z - z' \in B_{q+1}

page 183 line 6

ki = - ki = j
to
ki = -ik = j

page 189 line -6

\{\nu(\beta)\} \times \bar{W} \subset \bar{U}
to
\{\nu(\beta)\} \times \bar{W} \subset U'

page 191 line -6

left top corner of 2nd diagram U - \{0\}
to
U' - \{0\}

page 213 line -13

i\colon (X^{k-1},\emptyset) \hookrightarrow (X^{k},X^{k-1})
to
i\colon (X^{k-1},\emptyset) \hookrightarrow (X^{k-1},X^{k-2})

page 266 line -18

"Since \Delta^{p} \times \Delta^{p} is convex, we see that the model (\Delta^{p},\Delta^{p}) is F-acyclic."
to
"Since \Delta^{p} \times \Delta^{q} is convex, we see that the model (\Delta^{p},\Delta^{q}) is F-acyclic."

page 276 line 14

vw^{-1} = k^{-1}h
to
vw^{-1} = h^{-1}k

page 277 last line

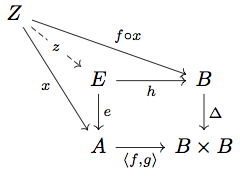
"Consider the diagram of continuous maps"
to
"Consider the \textbf{commutative} diagram of continuous maps"

page 288 line 15

"there exits a \textbf{unique} continuous h\colon \tilde{X} \to \tilde{Y} making the following diagram commute"
to
"there exits a continuous h\colon \tilde{X} \to \tilde{Y} making the following diagram commute"

Without specifying base points, there are many continuous maps making the diagram commute.

page 291 line 19

\theta\colon H \to G//H
to
\theta\colon X \to G//H

page 297 line 11

f_{t} = f_{t_{0}} * \lambda
to
f_{t} \sim f_{t_{0}} * \lambda

page 300 line -8

The sentence "Replacing V by V \cap U if necessary, we may assume that V \subset U." is verbose.
Since, F(V \times I) \subset U implies V = F(V \times \{0\}) \subset U.

page 302 line 12

"It is easy to see that \tilde{X}_{G} is a group with identity \tilde{e} and with [\bar{f}] the inverse of [f]"
to
"It is easy to see that \tilde{X}_{G} is a group with identity \tilde{e} and with {\langle \bar{f} \rangle}_{G} the inverse of {\langle f \rangle}_{G}"

page 308 line -4

"if U is open in X"
to
"if U is open in \tilde{X}/H"

page 313 line -12

x \in U \subset \bar{U} \subset W
to
y \in U \subset \bar{U} \subset W

page 318 line 10

Right parenthesis for (Hint\colon is missing.

page 323 line -15

"there are no cogroups in \textbf{hTop}"
to
"there are no non-trivial cogroups in \textbf{hTop}"

The empty set \emptyset is the trivial cogroup object in \textbf{hTop}.

page 324 line -3

In Lemma 11.6(i), Z is used to represent a space, but X is used in the proof.

page 331

I think the proof of the Theorem 11.12 is too concise or rather imprecise.

Suppose F\colon \Sigma X \to Y is a continuous map.
If we define \bar{F}\colon X \times I \to Y by \bar{F} = F \circ \nu where \nu\colon X \times I \to \Sigma X is a natural map,
then we can define \tau_{XY} by [F \to [\bar{F}^{\#}]].

In addition, if H\colon \Sigma X \times I \to Y is a (pointed) homotopy from F_{0} to F_{1}, association of H
is not a (pointed) homotopy from F_{0}^{\#} to F_{1}^{\#}.

So, first, we define \bar{H} by H \circ (\nu \times I) \circ u\colon X \times I \times I \to Y where
\nu is a natural map and u is a same map as in Theorem 11.8.
Then we can show that \bar{H}^{\#} is a (pointed) homotopy from \bar{F}_{0}^{\#} to \bar{F}_{1}^{\#}.

Similary, suppose G\colon X \to \Omega Y is a continuous map,
If we define \tilde{G^{\flat}}\colon \Sigma X \to Y by \tilde{G^{\flat}} = G^{\flat} \circ \nu^{-1},
then we can define {\tau_{XY}}^{-1} by [G] to [\tilde{G^{\flat}}].

If H\colon X \times I \to \Omega Y is a (pointed) homotopy from G_{0} to G_{1},
then we can show H^{\flat} \circ u \circ (\nu \times 1)^{-1} is a (pointed) homotopy from \tilde{G_{0}^{\flat}} to \tilde{G_{1}^{\flat}}.


I guess that it is hard to read this contents from the proof.

page 332 line 5

for all \omega, \omega' \in \Omega X
to
for all \omega, \omega' \in \Omega Y

page 334 line 9

\Sigma S^{n} = S^{n} \wedge S^{1} = (\textbf{R}^{n})^{\infty} \wedge \textbf{R}^{\infty} = (\textbf{R}^{n} \times \textbf{R})^{\infty} = (\textbf{R}^{n+1})^{\infty} = S^{n+1}
to
\Sigma S^{n} \approx S^{n} \wedge S^{1} \approx (\textbf{R}^{n})^{\infty} \wedge \textbf{R}^{\infty} \approx (\textbf{R}^{n} \times \textbf{R})^{\infty} = (\textbf{R}^{n+1})^{\infty} \approx S^{n+1}

page 336 line -4

"Recall the identities \dot{\textbf{I}}^{n} = (\dot{\textbf{I}}^{n-1} \times \textbf{I}) \cup (\textbf{I}^{n-1} \times \dot{\textbf{I}})
and (\textbf{I}^{n-1} \times \textbf{I})/(\dot{\textbf{I}}^{n-1} \times \textbf{I}) = (\textbf{I}^{n-1}/\dot{\textbf{I}}^{n-1}) \times \textbf{I}"

I guess the second identity does not hold.
When n = 2, (\textbf{I} \times \textbf{I})/(\dot{\textbf{I}} \times \textbf{I}) means that
for all s, (0,s) and (1,s) are identified to a single point.
On the other hand, (\textbf{I}/\dot{\textbf{I}}) \times \textbf{I} means that for each s, (0,s) and (1,s) is identified to a point,
but, for distinct s, s', [0,s] and [0,s'] are still distinct.

page 339 line -13

" \textit{Let} \alpha, \beta \in \mathcal{Q}(X,x_{0})."

In Lemma 11.23(i) \beta \in \mathcal{Q}(X,x_{0}), but, in Lemma 11,23(ii), \beta \in \mathcal{Q}(X,x_{1}).

page 347 line 17

(x_{0}, \omega_{0}, \beta)
to
(x_{0}, \omega_{0}, \beta^{-1})

page 348 line 7

\omega_{0} \simeq f
to
c \simeq f, where c is the constant map at y_{0}.

page 338 line -10

F\colon fg \simeq c rel x_{0}, where c is the constant map at x_{0}.
to
F\colon c \simeq fg rel z_{0}, where z_{0} is the base point of Z and c is the constant map at y_{0}.

The order of the homolopy F is sensitive, since it is used to define \phi\colon Z \to M(fg).

page 353 line -7

"Let \beta\colon (D^{n+1},S^{n}) \to (X, A) be a pointed map, and assume further that \beta(0) = x_{0}"

For \tilde{\beta} to be a pointed map, \tilde{\beta}(s_{n}) = (x_{0}, \omega_{s_{n}}) must be a base point of Mi,
namely, \omega_{s_{n}} must be a constant map at x_{0}.
So, the condition \beta(0) = x_{0} is not enough.
We need that for all t \in \textbf{I}, \omega_{s_{n}}(t) = \beta(ts_{n}) = x_{0}.

If \gamma(D^{n+1},S^{n}) \to (X,A) is any pointed map, there is a pointed pair homotopy \gamma \simeq \gamma \xi,
and \gamma \xi(ts_{n}) = x_{0}, since explicit formula of Lemma 11.41 is F(z,s) = z + (1 - |z|)ss_{n}, and F(ts_{n},1) = s_{n}.

This further condition does hold.

page 363 line 2

"Note that h is well defined (i.e., h(u,0) = x_{0} for all u \in S^{n-1})"

Why does this hold?
From the definition of h on D^{n} \times \{0\}, forall u \in S^{n-1}, h(u, 0) = f(u) \in F, and
generally f(u) \neq x_{0}.

I guess it works fine if we define h only on D^{n} \times \{0\}.

page 365 line 4

G(\{u\} \times [0, b_{1}])
to
G(\{u\} \times [0, t_{1}])

page 365 line 7

\tilde{h}_{0}\colon L^{(0)} \times [0,t] \to E
to
\tilde{h}_{0}\colon L^{(0)} \times [0,t_{1}] \to E

page 365 line 14

\tilde{\nu}_{\sigma}|\sigma \times \{0\} = \tilde{f}i|\sigma \times \{0\}
to
\tilde{\nu}_{\sigma}|\sigma \times \{0\} = \tilde{f}i^{-1}|\sigma \times \{0\}

page 365 line -8

h\sigma(u, t)
to
h^{\sigma}(u,t)

page 380 line 4

P = \{P_{n}\colon S_{n}(X) \to S_{n+1}(Y)\}
to
P = \{P_{n}\colon S_{n}(X) \to S_{n+1}(X \times \textbf{I})\}

page 382 line -6

"(Hint \colon If the projection \sum A_{\lambda} \to A_{\lambda} is denoted by p_{\lambda} and
if f \colon \sum A_{\lambda} \to G, then f \mapsto (p_{\lambda}f) is an isomorphism.)"
to
"(Hint \colon If the injection A_{\lambda} \to \sum A_{\lambda} is denoted by j_{\lambda} and
if f \colon \sum A_{\lambda} \to G, then f \mapsto (fj_{\lambda}) is an isomorphism.)"

page 387 line -8

F_{n}/F'_{n-1}
to
F_{n}/F'_{n}

page 387 line -3

\alpha' \in F'_{n}
to
\alpha' \in F'_{n-1}

page 403 line 4

"It can be shown that R \otimes S is the coproduct of R and S in the category of rings(or the category of graded ring)"
to
"It can be shown that R \otimes S is the coproduct of R and S in the category of \textbf{commutative} rings
(or the category of \textbf{commutative} graded ring)"

参考文献

An Introduction to Algebraic Topology (Graduate Texts in Mathematics)

An Introduction to Algebraic Topology (Graduate Texts in Mathematics)

Steve Awodey の Category Theory を読む : Chapter 6

数学 数学-圏論

Steve Awodey の Category Theory を読む シリーズトップ

6.2 Cartesian closed categories

Example 6.5

\omegaCPO はプログラミング言語の Denotational Semantics で使用される重要な代数構造なのでここでは詳しく証明しておきます。

Q^{P} is an \omegaCPO

任意の f_{0} \leq f_{1} \leq \cdots に対して、 \varinjlim_{i} f_{i} を任意の p \in P に対して \left( \varinjlim_{i} f_{i} \right)(p) = \varinjlim_{i} f_{i}(p) で定義します。この \varinjlim_{i} f_{i} が monotone かつ \omega-continuous であることを証明します。

Lemma
\varinjlim_{i} f_{i} \text{ is monotone}.

Proof.
任意の p, p' \in P と任意の i \in N に対して、 f_{i} が monotone であることより、 f_{i}(p) \leq f_{i}(p') \leq \varinjlim_{i} f_{i}(p') が成り立つ。よって colimit の UMP より \left( \varinjlim_{i} f_{i} \right)(p) = \varinjlim_{i} f_{i}(p) \leq \varinjlim_{i} f_{i}(p') = \left( \varinjlim_{i} f_{i} \right)(p') が成り立つ。

\square

次に \varinjlim_{i} f_{i} が \omega-continuous であることを証明するのですが、その前に準備として任意の f_{0} \leq f_{1} \leq \cdots と任意の p_{0} \leq p_{1} \leq \cdots に関して次の事柄を証明しておきます。

Lemma
\exists \varinjlim_{j} f_{0}(p_{j}) \leq \varinjlim_{j} f_{1}(p_{j}) \leq \cdots ,\, \exists \varinjlim_{i} \left( \varinjlim_{j} f_{i}(p_{j}) \right) ,\, \forall i,\, \varinjlim_{j} f_{i}(p_{j}) \leq \varinjlim_{i} \left( \varinjlim_{j} f_{i}(p_{j}) \right)

Proof.
任意の i に対して \varinjlim_{j} f_{i}(p_{j}) \leq \varinjlim_{j} f_{i+1}(p_{j}) を示せば、 \varinjlim_{j} f_{0}(p_{j}) \leq \varinjlim_{j} f_{1}(p_{j}) \leq \cdots が \omega chain となる。すると Q が \omegaCPO であることから残りの性質は明らかである。
f_{i}, f_{i+1} が \omega-continuous であることから、 f_{i}(\varinjlim_{j} p_{j}) \leq f_{i+1}(\varinjlim_{j} p_{j}) を示せばよいが、 f_{i} \leq f_{i+1} であるからこれは成り立つ。

\square

Lemma
\exists \varinjlim_{i} f_{i}(p_{0}) \leq \varinjlim_{i} f_{i}(p_{1}) \leq \cdots ,\, \exists \varinjlim_{j} \left( \varinjlim_{i} f_{i}(p_{j}) \right) ,\, \forall j,\, \varinjlim_{i} f_{i}(p_{j}) \leq \varinjlim_{j} \left( \varinjlim_{i} f_{i}(p_{j}) \right)

Proof.
任意の j に対して \varinjlim_{i} f_{i}(p_{j}) \leq \varinjlim_{i} f_{i}(p_{j+1}) を示せば、 \varinjlim_{i} f_{i}(p_{0}) \leq \varinjlim_{i} f_{i}(p_{1}) \leq \cdots が \omega chain となる。すると Q が \omegaCPO であることから残りの性質は明らかである。
\varinjlim_{i} f_{i} が monotone であることより \varinjlim_{i} f_{i}(p_{j}) = \left( \varinjlim_{i} f_{i} \right) (p_{j}) \leq \left( \varinjlim_{i} f_{i} \right) (p_{j+1}) = \varinjlim_{i} f_{i}(p_{j+1}) が成り立つ。

\square

Lemma
\varinjlim_{i} \left( \varinjlim_{j} f_{i}(p_{j}) \right) = \varinjlim_{j} \left( \varinjlim_{i} f_{i}(p_{j}) \right)

Proof.

  • \varinjlim_{i} \left( \varinjlim_{j} f_{i}(p_{j}) \right) \leq \varinjlim_{j} \left( \varinjlim_{i} f_{i}(p_{j}) \right)

任意の i と任意の j に対して f_{i} \leq \varinjlim_{i} f_{i} と上で示したことより f_{i}(p_{j}) \leq \varinjlim_{i} f_{i}(p_{j}) \leq \varinjlim_{j} \left( \varinjlim_{i} f_{i}(p_{j}) \right) が成り立つ。
すると \omega chain f_{i}(p_{0}) \leq f_{i}(p_{1}) \leq \cdots に対する colimit の UMP より \varinjlim_{j} f_{i}(p_{j}) \leq \varinjlim_{j} \left( \varinjlim_{i} f_{i}(p_{j}) \right) が成り立つ。
さらに上で示した \omega chain \varinjlim_{j} f_{0}(p_{j}) \leq \varinjlim_{j} f_{1}(p_{j}) \leq \cdots に対する colimit の UMP より \varinjlim_{i} \left( \varinjlim_{j} f_{i}(p_{j}) \right) \leq \varinjlim_{j} \left( \varinjlim_{i} f_{i}(p_{j}) \right) が成り立つ。

  • \varinjlim_{j} \left( \varinjlim_{i} f_{i}(p_{j}) \right) \leq \varinjlim_{i} \left( \varinjlim_{j} f_{i}(p_{j}) \right)

任意の j と任意の i に対して f_{i} が monotone であることと上で示したことより f_{i}(p_{j}) \leq \varinjlim_{j} f_{i}(p_{j}) \leq \varinjlim_{i} \left( \varinjlim_{j} f_{i}(p_{j}) \right) が成り立つ。
すると \omega chain f_{0}(p_{j}) \leq f_{1}(p_{j}) \leq \cdots に対する colimit の UMP より \varinjlim_{i} f_{i}(p_{j}) \leq \varinjlim_{i} \left( \varinjlim_{j} f_{i}(p_{j}) \right) が成り立つ。
さらに上で示した \omega chain \varinjlim_{i} f_{i}(p_{0}) \leq \varinjlim_{i} f_{i}(p_{1}) \leq \cdots に対する colimit の UMP より \varinjlim_{j} \left( \varinjlim_{i} f_{i}(p_{j}) \right) \leq \varinjlim_{i} \left( \varinjlim_{j} f_{i}(p_{j}) \right) が成り立つ。

\square

以上の準備を元に \varinjlim_{i} f_{i} が \omega-continuous であることを証明します。

Lemma
\varinjlim_{i} f_{i} \text{ is } \omega \text{-continuous}.

Proof.
\begin{align*}
\left( \varinjlim_{i} f_{i} \right) (\varinjlim_{j} p_{j}) &\underset{\text{def}}{=} \varinjlim_{i} f_{i} \left( \varinjlim_{j} p_{j} \right) \\
&\underset{f_{i} \text{ is continuous}}{=} \varinjlim_{i} \left( \varinjlim_{j} f_{i}(p_{j}) \right) \\
&= \varinjlim_{j} \left( \varinjlim_{i} f_{i}(p_{j}) \right) \\
&\underset{\text{def}}{=} \varinjlim_{j} \left( \left( \varinjlim_{i} f_{i} \right) (p_{j}) \right)
\end{align*}

\square

\epsilon is \omega-continuous

まず任意の \omega chain (f_{0}, p_{0}) \leq (f_{1}, p_{1}) \leq \cdots に関して以下の事柄を証明します。

Lemma
\varinjlim_{i} (f_{i}, p_{i}) = \left( \varinjlim_{j} f_{j}, \varinjlim_{k} p_{k} \right)

Proof.
任意の i に対して f_{i} \leq \varinjlim_{j} f_{j} かつ p_{i} \leq \varinjlim_{k} p_{k} が成り立つ。よって (f_{i}, p_{i}) \leq \left( \varinjlim_{j} f_{j}, \varinjlim_{k} p_{k} \right) が成り立つ。
任意の (x,y) と任意の i に対して (f_{i}, p_{i}) \leq (x, y) が成り立つとする。すると \omega chain f_{0} \leq f_{1} \leq \cdots に対する colimit の UMP より \varinjlim_{j} f_{j} \leq x が成り立つ。同様に \varinjlim_{k} p_{k} \leq y が成り立つ。よって \left( \varinjlim_{j} f_{j}, \varinjlim_{k} p_{k} \right) \leq (x, y) が成り立つので、 \varinjlim_{i} (f_{i}, p_{i}) = \left( \varinjlim_{j} f_{j}, \varinjlim_{k} p_{k} \right) である。

\square

Lemma
\epsilon \left( \varinjlim_{i} (f_{i}, p_{i}) \right) = \varinjlim_{i} \epsilon( f_{i}, p_{i})

Proof.
上で証明したことと \epsilon の定義より、証明するべきことは \left( \varinjlim_{j} f_{j} \right) \left( \varinjlim_{k} p_{k} \right) = \varinjlim_{i} f_{i}(p_{i}) である。

  • \varinjlim_{i} f_{i}(p_{i}) \leq \left( \varinjlim_{j} f_{j} \right) \left( \varinjlim_{k} p_{k} \right)

任意の i に対して、

\begin{align*}
f_{i}(p_{i}) &\underset{f_{i} \text{ is monotone}}{\leq} f_{i} \left( \varinjlim_{k} p_{k} \right) \\
&\leq \varinjlim_{j} \left( f_{j} \left( \varinjlim_{k} p_{k} \right) \right) \\
&\underset{\text{def}}{=} \left( \varinjlim_{j} f_{j} \right) \left( \varinjlim_{k} p_{k} \right)
\end{align*}

\omega chain f_{0}(p_{0}) \leq f_{1}(p_{1}) \leq \cdots に対する colimit の UMP より \varinjlim_{i} f_{i}(p_{i}) \leq \left( \varinjlim_{j} f_{j} \right) \left( \varinjlim_{k} p_{k} \right) が成り立つ。

  • \left( \varinjlim_{j} f_{j} \right) \left( \varinjlim_{k} p_{k} \right) \leq \varinjlim_{i} f_{i}(p_{i})

任意の j と任意の k に対して、 f_{j} (p_{k}) \leq \varinjlim_{i} f_{i}(p_{i}) を示す。
j \leq k のとき、
f_{j}(p_{k}) \leq f_{k}(p_{k}) \leq \varinjlim_{i} f_{i}(p_{i}) が成り立つ。
k \leq j のとき、
f_{j}(p_{k}) \leq f_{j}(p_{j}) \leq \varinjlim_{i} f_{i}(p_{i}) が成り立つ。
よって \omega chain f_{j}(p_{0}) \leq f_{j}(p_{1}) \leq \cdots に対する colimit の UMP より \varinjlim_{k} f_{j}(p_{k}) \leq \varinjlim_{i} f_{i}(p_{i}) が成り立つ。これは f_{j} が continuous であることより f_{j} \left( \varinjlim_{k} p_{k} \right) \leq \varinjlim_{i} f_{i}(p_{i}) と同値である。
すると \omega chain f_{0} \left( \varinjlim_{k} p_{k} \right) \leq f_{1} \left( \varinjlim_{k} p_{k} \right) \leq \cdots に対する colimit の UMP より \varinjlim_{j} f_{j} \left( \varinjlim_{k} p_{k} \right) \leq \varinjlim_{i} f_{i}(p_{i}) が成り立つ。定義より \left( \varinjlim_{j} f_{j} \right) \left( \varinjlim_{k} p_{k} \right) \leq \varinjlim_{i} f_{i}(p_{i}) である。

\square

\tilde{f} is \omega-continuous if f is so

任意の \omega chain x_{0} \leq x_{1} \leq \cdots に対して、以下の事柄を証明します。

Lemma
\tilde{f} \left( \varinjlim_{i} x_{i} \right) = \varinjlim_{i} \tilde{f}(x_{i})

Proof.
任意の p \in P に対して \tilde{f} \left( \varinjlim_{i} x_{i} \right)(p) = \left( \varinjlim_{i} \tilde{f}(x_{i}) \right)(p) を示せばよいが、これは \tilde{f} の定義より f \left( \varinjlim_{i} x_{i}, p \right) = \varinjlim_{i} f(x_{i}, p) と同値である。
\omega chain (x_{0},p) \leq (x_{1}, p) \leq \cdots に対して、上で証明したことより \varinjlim_{i} (x_{i}, p) = \left( \varinjlim_{i} x_{i}, p \right) が成り立つ。
よって f が \omega-continuous であることより f \left( \varinjlim_{i} x_{i}, p \right) = f \left( \varinjlim_{i} (x_{i}, p) \right) = \varinjlim_{i} f(x_{i}, p) が成り立つ。

\square

Example 6.6

初めにテキストの通りに定義された \epsilon が graph homomorphism であることを証明します。

Lemma
\epsilon \colon H^{G} \times G \to H \text{ is a graph homomorphism}.

Proof.
f:id:hitotakuchan:20160516120426p:plain
上の diagram が可換になることを示せばよい。
任意の \theta \colon \phi \to \psi \in {H^{G}}_{e} と任意の e \in G_{e} に対して、 (s \circ \epsilon_{e})(\theta, e) = s(\theta(e)) = \phi(s(e)) が成り立つ。さらに、 (\epsilon_{v} \circ s)(\theta, e) = \epsilon_{v}(s(\theta), s(e)) = \epsilon_{v}(\phi, s(e)) = \phi(s(e)) が成り立つ。よって s \circ \epsilon_{e} = \epsilon_{v} \circ s が成り立つ。
同様に t \circ \epsilon_{e} = \epsilon_{v} \circ t が成り立つ。

\square

次に H^{G} が exponential object in \bf{Graphs} であることを証明します。

Lemma
H^{G} \text{ is an exponential object in } \bf{Graphs}.

Proof.
初めに、任意の f \colon F \times G \to H に対してテキストの通りに定義される \tilde{f} \colon F \to H^{G} が graph homomorphism となることを証明する。それには次の diagram が可換となることを示せばよい。
f:id:hitotakuchan:20160516122209p:plain
これは任意の c \colon a \to b \in F_{e} に対して、 \tilde{f}_{e}(c) \colon \tilde{f}_{v}(a) \to \tilde{f}_{v}(b) \colon \in H^{G}_{e} となることと同値であり、さらに H^{G} の定義より以下の diagram が可換になることと同値である。
f:id:hitotakuchan:20160516123743p:plain
任意の e \in G_{e} に対して、 \left( s \circ \tilde{f}_{e}(c) \right)(e) = s(f_{e}(c,e)) = f_{v}(s(c,e)) = f_{v}(a,s(e)) = \left( \tilde{f}_{v}(a) \right)(s(e)) = \left( \tilde{f}_{v}(a) \circ s \right)(e) が成り立つ。同様に \left( t \circ \tilde{f}_{e}(c) \right)(e) = \left( \tilde{f}_{v}(b) \circ t \right)(e) が成り立つ。よって \tilde{f} は graph homomorphism である。
この \tilde{f} に対して \epsilon \circ \left( \tilde{f} \times 1 \right) = f が成り立つことは明らかである。
次に任意の f' \colon F \to H^{G} が \epsilon \circ (f' \times 1) = f を満たすとする。
任意の a \in F_{v} と任意の u \in G_{v} に対して f'_{v}(a)(u) = (\epsilon \circ (f' \times 1))(a, u) = f_{v}(a, u) = \tilde{f}_{v}(a)(u) が成り立つ。
また、任意の c \in F_{e} と任意の e \in G_{e} に対して f'_{e}(c)(e) = (\epsilon \circ (f' \times 1))(c, e) = f_{e}(c, e) = \tilde{f}_{e}(c)(e) が成り立つ。よって f' = \tilde{f} が成り立つ。

\square

6.3 Heyting Algebras

Definition 6.10

lattice に関しては complete であることと cocomplete であることが同値であることを証明します。
さらっと書かれていますが、その前の poset P がすべての set-indexed meets を持てば、圏論的な意味で complete となるということの証明はできますか？
set-indexed meets を持つというのは、任意の集合 I を離散圏とみなした場合に任意の diagram D \colon I \to P が limit を持つことと言い換えられます。一方で、圏論的な意味で complete になるためには任意の diagram に対して limit を持たないといけません。
poset を圏とみなした場合、任意の対象間にはただ一つしか arrow が存在しないということから証明できます。

Lemma
\text{A lattice } (L, \leq) \text{ is complete} \Rightarrow (L, \leq) \text{ is cocomplete}.

Proof.
任意の I-index 集合 \left\{ a_{i} \in L \right\} に対して、集合 I' を I' = \left\{ b \in L \, \middle| \, \forall i \in I,\, a_{i} \leq b \right\} で定義する。すると、 L が complete であることから、 I' の limit \bigwedge_{b \in I'} b が存在する。これが \left\{ a_{i} \right\} の colimit \bigvee_{i \in I} a_{i} であることを示す。
任意の i \in I と任意の b \in I' に対して I' の定義より a_{i} \leq b が成り立つ。すると、 \bigwedge_{b \in I'} b は I' の limit であるから limit の UMP より a_{i} \leq \bigwedge_{b \in I'} b が成り立つ。
次に、任意の x \in L が任意の i \in I に対して a_{i} \leq x を満たすとする。すると I' の定義より x \in I' が成り立つ。よって limit の定義より \bigwedge_{b \in I'} b \leq x が成り立つ。
poset の anti-symmetricity より \bigvee_{i \in I} a_{i} = \bigwedge_{b \in I'} b である。

\square

6.7 Variable sets

6.7.1 において証明が省略されている事柄は exercise 15 としてまとめられているので、そちらの証明をしておきます。

Exercise 15(a)

Lemma
{\bf{2}}^{I} \text{ is a Heyting algebra}.

Proof.

  • {\bf{2}}^{I} has a terminal object 1

1 を任意の i \in I に対して 1(i) = \top で定義すると、任意の f \in {\bf{2}}^{I} と任意の i \in I に対して、 f(i) \leq 1(i) が成り立つので f \leq 1 が成り立つ。

  • {\bf{2}}^{I} has products

任意の f,g \in {\bf{2}}^{I} に対して f \land g を任意の i \in I に対して (f \land g)(i) = f(i) \land g(i) で定義する。すると f \land g \leq f かつ f \land g \leq g が成り立つ。このとき f \land g が product となることを示す。
任意の h \in {\bf{2}}^{I} に対して h \leq f かつ h \leq g が成り立つとすると、任意の i \in I に対して h(i) \leq f(i) \land g(i) が成り立つので、 h \leq f \land g が成り立つ。 {\bf{2}}^{I} が poset であることより、これはただ一つに決まる。

  • {\bf{2}}^{I} has an initial object 0

0 を任意の i \in I に対して 0(i) = \bot で定義すれば、任意の f \in {\bf{2}}^{I} に対して 0 \leq f が成り立つ。

  • {\bf{2}}^{I} has coproducts

任意の f,g \in {\bf{2}}^{I} に対して f \lor g を任意の i \in I に対して (f \lor g)(i) = f(i) \lor g(i) で定義する。すると product の場合と同様に f \lor g は coproduct となる。

  • {\bf{2}}^{I} has exponentials

任意の f, g \in {\bf{2}}^{I} に対して f \Rightarrow g を任意の i \in I に対して (f \Rightarrow g)(i) = \top \iff \forall j \leq i,\, f(j) \leq g(j) で定義する。

f \land g \leq h ならば f \leq g \Rightarrow h が成り立つこと。
任意の i \in I に対して f(i) \leq (g \Rightarrow h)(i) を示せばよい。 f(i) = \bot ならば f(i) \leq (g \Rightarrow h)(i) は明らかである。 f(i) = \top とすると、任意の j \geq i に対して g(j) \leq h(j) を示せばよいが、仮定より f(j) \land g(j) \leq h(j) が成り立つ。また f が monotone であることより f(j) = \top が成り立つ。よって g(j) \leq h(j) が成り立つ。

f \leq g \Rightarrow h ならば f \land g \leq h が成り立つこと。
任意の i \in I に対して f(i) \land g(i) \leq h(i) を示せばよい。 f(i) = \bot ならば f(i) \land g(i) \leq h(i) は明らかである。 f(i) = \top とすると g(i) \leq h(i) が成り立つことを示せばよい。仮定より f(i) \leq g(i) \Rightarrow h(i) が成り立つが、 f(i) = \top より g(i) \Rightarrow h(i) = \top である。よって exponential の定義より g(i) \leq h(i) が成り立つ。

\square

Exercise 15(b)

Lemma
y(a) \text{ is monotone}.

Proof.
任意の x \leq y \in A^{op} に対して y(a)(x) \leq y(a)(y) \in {\bf{2}} を示せばよい。 y(a)(x) = \top の場合を考えれば十分である。このとき x \leq a \in A が成り立つ。また x \leq y \in A^{op} ならば y \leq x \in A が成り立つので y \leq a \in A が成り立つ。よって y(a)(y) = \top となるので y(a)(x) \leq y(a)(y) が成り立つ。

\square

Lemma
y \text{ is monotone}.

Proof.
任意の a \leq b \in A に対して y(a) \leq y(b) \in {\bf{2}}^{I} を示す。任意の x \in A^{op} に対して y(a)(x) = \top とすると x \leq a \in A が成り立つ。 a \leq b \in A より x \leq b \in A が成り立つので y(b)(x) = \top となる。よって y(a) \leq y(b) \in {\bf{2}}^{I} が成り立つ。

\square

Lemma
y \text{ is injective}.

Proof.
任意の a,b \in A に対して y(a) = y(b) が成り立つとする。このとき任意の x \in A^{op} に対して y(a)(x) = y(b)(x) が成り立つ。 x = a とすると y(a)(a) = \top より y(b)(a) = \top が成り立ち a \leq b \in A が成り立つ。同様に x = b とすると b \leq a \in A が成り立つので a = b となる。

\square

Lemma
y \text{ preserves CCC structure}.

Proof.

  • preserves terminal object 1

任意の x \in A^{op} に対して y(1)(x) = \top が成り立つので y(1) = 1 \in {\bf{2}}^{I} である。

  • preserves products

任意の a,b \in A と任意の x \in A^{op} に対して y(a \land b)(x) = \left( y(a) \land y(b) \right)(x) を示せばよい。つまり x \leq a \land b \iff x \leq a \land x \leq b \in A を示せばよいが、これは a \land b が product であることより明らかである。

  • preserves exponentials

任意の a,b \in A と任意の x \in A^{op} に対して y(a \Rightarrow b)(x) = \left( y(a) \Rightarrow y(b) \right)(x) を示せばよい。つまり x \leq a \Rightarrow b \iff \forall y \geq x \in A^{op},\, y(a)(y) \leq y(b)(y) を示せばよい。

only if case
y \leq a \in A とすると x \leq y \in A^{op} より y \leq x \in A であるから、 y \leq x \land a が成り立つ。一方、仮定より x \leq a \Rightarrow b であるから x \land a \leq b が成り立つ。よって y \leq b \in A となるので y(a)(y) \leq y(b)(y) が成り立つ。

if case
x \land a \leq x \in A が成り立つことから x \leq x \land a \in A^{op} が成り立つ。すると仮定より y(a)(x \land a) \leq y(b)(x \land a) が成り立つ。 x \land a \leq a \in A は常に成り立つので、 y(a)(x \land a) = \top となるから y(b)(x \land a) = \top つまり x \land a \leq b \in A が成り立つ。よって x \leq a \Rightarrow b が成り立つ。

\square

参考書籍

Category Theory (Oxford Logic Guides)

Category Theory (Oxford Logic Guides)

  • 作者:Awodey, Steve
  • 発売日: 2008/01/10
  • メディア: ペーパーバック
圏論 原著第2版

圏論 原著第2版

Steve Awodey の Category Theory を読む : Chapter 5

数学 数学-圏論

Steve Awodey の Category Theory を読む シリーズトップ

5.2 Pullbacks

Proposition 5.5

only if case しか証明されていないので、if case の証明を補っておきます。

Lemma
(E, p_{1}, p_{2}) \text{ is a pullback of } f \text{ and } g \Rightarrow (E, \left< p_{1}, p_{2} \right>) \text{ is an equalizer of } f \circ \pi_{1} \text{ and } g \circ \pi_{2}.

Proof.
任意の z \colon Z \to A \times B に対して、 f \circ \pi_{1} \circ z = g \circ \pi_{2} \circ z が成り立つとする。 (E, p_{1}, p_{2}) が pullback であることより、 \exists !\,u \colon Z \to E が存在して p_{1} \circ u = \pi_{1} \circ z かつ p_{2} \circ u = \pi_{2} \circ z を満たす。
このとき、 i = 1,2 に対して、 \pi_{i} \circ \left< p_{1}, p_{2} \right> \circ u = p_{i} \circ u = \pi_{i} \circ z であるから、 A \times B の UMP より \left< p_{1}, p_{2} \right> \circ u = z が成り立つ。
次に、任意の u' \colon Z \to E に対して、 \left< p_{1}, p_{2} \right> \circ u' = z が成り立つすると、 i = 1,2 に対して p_{i} \circ u' = \pi_{i} \circ \left< p_{1}, p_{2} \right> \circ u' = \pi_{i} \circ z = p_{i} \circ u が成り立つ。よって pullback の UMP より u' = u が成り立つ。

\square

Exercise 3

Lemma
m \text{ is monic} \Rightarrow m' \text{ is monic}.

Proof.
f:id:hitotakuchan:20160502130742p:plain
任意の z_{1}, z_{2} \colon Z \to M' に対して、 m' \circ z_{1} = m' \circ z_{2} が成り立つとする。このとき、 m \circ f' \circ z_{1} = f \circ m' \circ z_{1} = f \circ m' \circ z_{2} = m \circ f' \circ z_{2} が成り立つが、 m が monic であることより f' \circ z_{1} = f' \circ z_{2} が成り立つ。
M' が pullback であることより、 \exists !\,z \colon Z \to M' が存在して、 m' \circ z = m' \circ z_{1} = m' \circ z_{2} かつ f' \circ z = f' \circ z_{1} = f' \circ z_{2} を満たすが、 z_{1},z_{2} も diagram を可換にするので z_{1} = z = z_{2} が成り立つ。よって m' は monic である。

\square

5.3 Properties of pullbacks

Two pullbacks lemma

Lemma
\text{If the two squares are pullbacks, so is the outer rectangle}.

Proof.
f:id:hitotakuchan:20160503121002p:plain
任意の x \colon Z \to A と y \colon Z \to D に対して、 g \circ f \circ x = h \circ y が成り立つとする。すると right square が pullback であることより、 \exists !\, z' \colon Z \to E が存在して g' \circ z' = y かつ h' \circ z' = f \circ x を満たす。さらに left square が pullback であることより \exists !\, z \colon Z \to F が存在して h'' \circ z = x かつ f' \circ z = z' を満たす。
次に、任意の z'' \colon Z \to F に対して h'' \circ z'' = x かつ g' \circ f' \circ z'' = y が成り立つとする。 f' \circ z'' は g' \circ (f' \circ z'') = y と h' \circ (f' \circ z'') = f \circ h'' \circ z'' = f \circ x が成り立つから、right square の UMP より f' \circ z'' = z' が成り立つ。すると left square の UMP より z = z'' が成り立つ。

\square

Lemma
\text{If the right square and the outer rectangle are pullbacks, so is the left square}.

Proof.
f:id:hitotakuchan:20160503121025p:plain
任意の x \colon Z \to A と y \colon Z \to E に対して、 f \circ x = h' \circ y とする。 g \circ f \circ x = g \circ h' \circ y = h \circ g' \circ y が成り立ち、outer rectangle が pullback であることより \exists !\, z \colon Z \to F が存在して h'' \circ z = x かつ g' \circ f' \circ z = g' \circ y を満たす。
h' \circ f' \circ z = f \circ h'' \circ z = f \circ x = h' \circ y が成り立つことと、right square が pullback であることより f' \circ z = y が成り立つ。
次に、任意の z' \colon Z \to F に対して h'' \circ z' = x かつ f' \circ z' = y が成り立つとする。すると g' \circ f' \circ z' = g' \circ y が成り立つので、outer rectangle の UMP より z = z' が成り立つ。

\square

Proposition 5.10

証明自体は難しくないので詳細は省略します。一般に pullback は up to isomorphism でしか決まりません。よって、この functor h^{\ast} の存在を言うためには選択公理を仮定するか、後で出てくる skeletal という概念を用いて圏 \bf{C} は skeletal であるという条件を付け加えないといけないと思います。

Example 5.13

Lemma
{\coprod_{j \in J} A_{\alpha(j)}} \text{ is a pullback}.

Proof.
f:id:hitotakuchan:20160503141325p:plain
\alpha'(j, a) = (\alpha(j), a) で定義する。 a \in A_{\alpha(j)} であるから \alpha' は well-defined である。
任意の f \colon Z \to J と g \colon Z \to {\coprod_{i \in I} A_{i}} に対して、 \alpha \circ f = p \circ g が成り立つとする。このとき、任意の z \in Z に対して g(z) = (i, a) とするとき、 h \colon Z \to {\coprod_{j \in J} A_{\alpha(j)}} を h(z) = (f(z), a) で定義する。これは \alpha(f(z)) = (\alpha \circ f)(z) = (p \circ g)(z) = i が成り立つので a \in A_{\alpha(f(z))} となり well-defined である。また、 (q \circ h)(z) = f(z) かつ (\alpha' \circ h)(z) = (\alpha(f(z)), a) = (i, a) = g(z) が成り立つので、 h は diagram を可換にする。
次に、任意の h' \colon Z \to {\coprod_{j \in J} A_{\alpha(j)}} が q \circ h' = f かつ \alpha' \circ h' = g を満たすとする。任意の z \in Z に対して h'(z) = (j, b) とすると、 q \circ h' = f より j = f(z) が成り立つ。また g(z) = (i, a) とすると、 (i,a) = g(z) = (\alpha' \circ h')(z) = (\alpha(f(z)), b) = (p(g(z)), b) = (i, b) より a = b が成り立つ。よって h = h' が成り立つ。

\square

5.4 Limits

Proposition 5.14

上の two-pullback lemma の場合もそうでしたが、証明が easy diagram chase とだけ書かれていて省略されている場合、私の経験上全然 easy じゃないことが多いので補足しておきます。

Lemma
(E,e,h) \text{ is a pullback then } (E,e) \text{ is an equalizer of } f,g.

Proof.
f:id:hitotakuchan:20160506130719p:plain
初めに \Delta が monic であることを示す。
任意の x,y \colon Z \to B に対して、 \Delta \circ x = \Delta \circ y が成り立つとする。すると x = 1_{B} \circ x = \pi_{1} \circ \Delta \circ x = \pi_{1} \circ \Delta \circ y = 1_{B} \circ y = y が成り立つ。よって \Delta は monic である。
次に、 f \circ e = \pi_{1} \circ \left< f,g \right> \circ e = \pi_{1} \circ \Delta \circ h = h と g \circ e = \pi_{2} \circ \left< f,g \right> \circ e = \pi_{2} \circ \Delta \circ h = h が成り立つので、 f \circ e = g \circ e が成り立つ。
最後に、任意の x \colon Z \to A に対して、 f \circ x = g \circ x が成り立つとする。このとき \pi_{1} \circ \Delta \circ f \circ x = f \circ x = \pi_{1} \circ \left< f,g \right> \circ x かつ \pi_{2} \circ \Delta \circ f \circ x = f \circ x = g \circ x = \pi_{2} \circ \left< f,g \right> \circ x が成り立つから B \times B の UMP より \Delta \circ f \circ x = \left< f,g \right> \circ x が成り立つ。すると Z が pullback であることより、 \exists !\, z \colon Z \to E が存在して e \circ z = x かつ h \circ z = f \circ x を満たす。
Exercise 3 より \Delta が monic なら e は monic となるので e \circ z = x を満たす z はただ一つに決まる。よって (E,e) は f と g の equalizer である。

\square

5.6 Colimits

Direct limits of groups

G_{\inf} が \omega-colimits であることの証明は簡単ではないです。ここでは詳細は証明は省略しますが、以下の記事で R 加群の場合の direct limit に関する基本的な性質の証明を行っているので、詳しく証明を確認したい人は参照してください。

www.orecoli.com

参考書籍

Category Theory (Oxford Logic Guides)

Category Theory (Oxford Logic Guides)

  • 作者:Awodey, Steve
  • 発売日: 2008/01/10
  • メディア: ペーパーバック
圏論 原著第2版

圏論 原著第2版

Steve Awodey の Category Theory を読む : Chapter 4

数学 数学-圏論

Steve Awodey の Category Theory を読む シリーズトップ

4.1 Groups in a category

Corollary 4.6

任意の (G,\circ,i,u) が abelian group であるとすると、 \circ、 i、 u が group homomorphism であれば (G, \circ, i, u) が group object であるための条件を満たすことは (G, \circ, i, u) が abelian group であることから明らかです。
\bf{Group} において 1 は zero object なので u \colon G \to 1 \to G はただ一つ存在する group homomorphism になります。そこで \circ と i が group homomorphism であることを証明します。

Lemma
\circ \text{ is a group homomorphism}.

Proof.
任意の (g_{1}, g_{2}), (h_{1},h_{2}) \in G \times G に対して、 (G,\circ,i,u) が abelian group であることより、

\begin{align*}
\circ((g_{1},g_{2}) \circ (h_{1}, h_{2}) ) &= \circ (g_{1} \circ h_{1}, g_{2} \circ h_{2}) \\
&= g_{1} \circ h_{1} \circ g_{2} \circ h_{2} \\
&= g_{1} \circ g_{2} \circ h_{1} \circ h_{2} \\
&= (\circ(g_{1}, g_{2}) ) \circ (\circ(h_{1}, h_{2}) )
\end{align*}

が成り立つので \circ は group homomorphism である。

\square

Lemma
i \text{ is a group homomorphism}.

Proof.
任意の g_{1}, g_{2} \in G に対して、 (G,\circ,i,u) が abelian group であることより、 i(g_{1} \circ g_{2}) = i(g_{2}) \circ i(g_{1}) = i(g_{1}) \circ i(g_{2}) が成り立つので i は group homomorphism である。

\square

4.2 The category of groups

\sim is an equivalence relation

group N が group G の subgroup であるとは任意の g_{1},g_{2} \in N に対して、 g_{1} \cdot g_{2}^{-1} \in N が成り立つこととして定義されます。この定義から N が G の単位元を自身の単位元として含むことが証明できます。
さらに N が G の normal subgroup であるとは、任意の g \in G と任意の h \in N に対して、 g \cdot h \cdot g^{-1} \in N が成り立つこととして定義されます。

Lemma
\sim \text{ is an equivalence relation}.

Proof.

  • reflexive

任意の h \in N に対して、 h \cdot h^{-1} = u \in N であるから、 h \sim h が成り立つ。

  • symmetric

任意の x,y \in N に対して x \sim y とすると、 x \cdot y^{-1} \in N が成り立つ。 N は group であるから、 (x \cdot y^{-1})^{-1} = y \cdot x^{-1} \in N が成り立つので y \sim x が成り立つ。

  • transitive

任意の x, y, z \in N に対して x \sim y かつ y \sim z とする。 x \cdot y^{-1} \in N と y \cdot z^{-1} \in N より x \cdot y^{-1} \cdot y \cdot z^{-1} = x \cdot z^{-1} \in N が成り立つ。よって x \sim z が成り立つ。

\square

Corollary 4.11

N = \text{ker}(h) であるとき、 \overline{h} が injective になることは書籍で証明されているので、ここでは h が injective であるための必要十分条件が \text{ker}(h) = \left\{ u \right\} であることを証明します。準備として以下を証明しておきます。

Lemma
h \text{ is injective} \iff \pi \text{ is injective}.

Proof.

  • only if case

任意の x,y \in G に対して、 [x] = [y] であるとする。このとき、 h(x) = \overline{h}([x]) = \overline{h}([y]) = h(y) が成り立つが、 h が injective であることより x = y が成り立つ。よって \pi は injective である。

  • if case

任意の x,y \in G に対して、 h(x) = h(y) であるとする。 h = \overline{h} \circ \pi であるから \overline{h}([x]) = \overline{h}([y]) が成り立つが、 \overline{h} が injective であるから [x] = [y] が成り立つ。さらに \pi が injective であるから x = y が成り立つ。よって h は injective である。

\square

この準備の元に次の補題を証明します。

Lemma
\pi \text{ is injective} \iff \text{ker}(h) = \left\{ u \right\}

Proof.

  • only if case

背理法により証明する。 \text{ker}(h) \neq \left\{ u \right\} であるとすると、 \exists x \in \text{ker}(h),\, x \neq u が存在する。すると x \cdot u \in \text{ker}(h) より [x] = [u] が成り立つ。仮定より \pi が injective であるから x = u が成り立つが、これは x \neq u と矛盾する。よって \text{ker}(h) = \left\{ u \right\} である。

  • if case

任意の x,y \in G に対して、 [x] = [y] であるとすると、 x \cdot y^{-1} \in \text{ker}(h) = \left\{ u \right\} が成り立つ。よって x = y となるので、 \pi は injective である。

\square

Cokernels are special coequalizers

Cokernel に関しては Exercise 5 を通して見ておきましょう。Exercise 5 では abelian group を考えているので、二項演算子を +、単位元を 0 で表します。
任意の f \colon A \to B に対して、 \pi \colon B \to B / \text{im}(f) を \pi(b) = [b] で定義される natural homomorphism であるとします。

f:id:hitotakuchan:20160411185847p:plain

Exercise\ 5\ (a)
Proof.
任意の a \in A に対して、 \pi \circ f (a) = [f(a)] で f(a) - 0_{B} \in \text{im}(f) であるから [f(a)] = [0_{B}] が成り立つ。 B/\text{im}(f) の単位元は [0_{B}] であるから \pi \circ f = 0_{B/\text{im}(f)} が成り立つ。
また任意の g \colon B \to G に対して、 g \circ f = 0_{G} が成り立つとする。 \overline{g} \colon B/\text{im}(f) \to G を \overline{g}([b]) = g(b) で定義する。このとき、 [b] = [b'] とすると b - b' \in \text{im}(f) より \exists a \in A,\, b - b' = f(a) が存在する。すると g(b) - g(b') = g(b - b') = g(f(a)) = 0_{G} が成り立つ。よって \overline{g} は well-defined である。
g = \overline{g} \circ \pi が成り立つことは定義より明らか。また \pi が epic であるから、 \overline{g} はただ一つに決まる。

\square

(a) で証明した UMP より、 (\pi, B/\text{im}(f) ) は f \colon A \to B と 0 \colon A \to 0 \to B の coequalizer であることがわかります。
次に cokernel を使用すると任意の coequalizer が構成できることを証明します。

f:id:hitotakuchan:20160411190220p:plain

Exercise\ 5\ (b)
Proof.
任意の f,f' \colon A \to B に対して、 f - f' を (f - f')(a) = f(a) - f'(a) で定義すると、 B が abelian group であることより

\begin{align*}
(f-f')(a + b) &= f(a + b) - f'(a + b) \\
&= f(a) + f(b) - f'(a) - f'(b) \\
&= f(a) - f'(a) + f(b) - f'(b) \\
&= (f-f')(a) + (f-f')(b)
\end{align*}

が成り立つので group homomorphism になる。 f - f' の cokernel を \pi \colon B \to B/\text{im}(f-f') とすると、 \pi が f、 f' の coequalizer となることを示す。
まず、 \pi \circ (f - f') = 0 より \pi \circ f = \pi \circ f' が成り立つ。
次に、任意の g \colon B \to G に対して、 g \circ f = g \circ f' が成り立つとする。このとき g \circ (f - f') = (g \circ f) - (g \circ f') = 0_{G} = g \circ 0_{B} が成り立つ。すると (a) で示した UMP より \exists ! \,\overline{g} \colon B/\text{im}(f) \to G が存在して、 g = \overline{g} \circ \pi が成り立つ。よって (\pi, B/\text{im}(f-f') ) は f と f' の coequalizer である。

\square

(c) に関しては以下の可換図式より \text{Ker}(\text{cok}(f) ) \cong A/\text{Ker}(f) であることを確認してください。可換図式では f の cokernel となる対象を \text{Cok}(f)、cokernel への homomorphism を \text{cok}(f) 等として表しています。

f:id:hitotakuchan:20160411191918p:plain

4.3 Groups as categories

composition of the congruence category is well-defined

\circ_{{\bf{C}}^{\sim}} を \left< f',g' \right> \circ_{{\bf{C}}^{\sim}} \left< f,g \right> = \left< f' \circ f, g' \circ g \right> で定義するとき、 \circ_{{\bf{C}}^{\sim}} が well-defined であることを証明します。

Lemma
\circ_{{\bf{C}}^{\sim}} \text{ is well-defined}.

Proof.
任意の f \sim g \colon A \to B と f' \sim g' \colon B \to C に対して、congruence の条件より f' \circ f = f' \circ f \circ 1_{A} \sim f' \circ g \circ 1_{A} = f' \circ g が成り立つ。一方で f' \circ g = 1_{C} \circ f' \circ g \sim 1_{C} \circ g' \circ g = g' \circ g が成り立つ。 \sim が equivalence relation であることより、 f' \circ f \sim g' \circ g が成り立つ。

\square

\sim_{F} is a congruence

\sim_{F} が equivalence relation であることは定義よりほぼ自明なので省略します。 \sim_{F} が congruence の条件を満たすことを証明します。

Lemma
\sim_{F} \text{ is a congruence}.

Proof.
任意の f,g \in {\bf{C}}_{1} に対して、 f \sim_{F} g とすると定義より \text{dom}(f) = \text{dom}(g) かつ \text{cod}(f) = \text{cod}(g) が成り立つ。
また任意の a \colon A \to \text{dom}(f) と b \colon \text{cod}(f) \to B に対して、 \text{dom}(b \circ f \circ a) = \text{dom}(a) = \text{dom}(b \circ g \circ a) かつ \text{cod}(b \circ f \circ a) = \text{cod}(b) = \text{cod}(b \circ g \circ a) が成り立つ。また F が functor であることより、 F(b \circ f \circ a) = F(b) \circ F(f) \circ F(a) = F(b) \circ F(g) \circ F(a) = F(b \circ g \circ a) が成り立つので、 b \circ f \circ a \sim_{F} b \circ g \circ a が成り立つ。よって \sim_{F} は congruence である。

\square

Theorem 4.13

Theorem 4.13 の証明は難しくないのですが省略されているのでここで証明しておきます。

Theorem
(\forall f,g \in {\bf{C}}_{1},\, f \sim g \Rightarrow f \sim_{F} g) \iff \exists !\, \tilde{F} \colon {\bf{C}}/\sim \, \to {\bf{D}},\, F = \tilde{F} \circ \pi

Proof.

  • only if case

\tilde{F} を \tilde{F}_{0}(C) = F(C)、 \tilde{F}_{1}([f]) = F(f) で定義する。このとき、任意の f,g \in {\bf{C}}_{1} に対して [f] = [g] であるとすると、 f \sim g であるから、仮定より f \sim_{F} g が成り立つ。よって定義より F(f) = F(g) が成り立つので、 \tilde{F}_{1} は well-defined である。
次に \tilde{F} が functor であることを示す。
\tilde{F}_{1}([f] \colon A \to B) = F(f) \colon F(A) \to F(B) = F(f) \colon \tilde{F}_{0}(A) \to \tilde{F}_{0}(B) であるから、 \tilde{F} は functor の条件 (a) を満たす。
また、 \tilde{F}_{1}([id] \colon A \to A) = F(id) = id_{F(A)} = id_{\tilde{F}_{0}(A)} が成り立つので、 \tilde{F} は functor の条件 (b) を満たす。
最後に \tilde{F}_{1}([f'] \circ [f]) = \tilde{F}_{1}([f' \circ f]) = F(f' \circ f) = F(f') \circ F(f) = \tilde{F}_{1}([f']) \circ \tilde{F}_{1}([f]) が成り立つので、 \tilde{F} は functor の条件 (c) を満たす。
よって \tilde{F} は functor である。
この \tilde{F} が F = \tilde{F} \circ \pi を満たすことは定義より明らかである。また \pi が epic であることより、 \tilde{F} はただ一つに決まる。

  • if case

f \sim g であるとすると、congruence の条件より \text{dom}(f) = \text{dom}(g) かつ \text{cod}(f) = \text{cod}(g) が成り立つ。さらに [f] = [g] であるから、 F(f) = (\tilde{F} \circ \pi)(f) = \tilde{F}([f]) = \tilde{F}([g]) = (\tilde{F} \circ \pi)(g) = F(g) が成り立つので f \sim_{F} g が成り立つ。

\square

Lemma
\tilde{F} \colon {\bf{C}}/\text{ker}(F) \to D \text{ is a faithful functor}.

Proof.
任意の [f],[g] \colon A \to B に対して \tilde{F}([f]) = \tilde{F}([g]) \Rightarrow [f] = [g] を示せばよい。 [f],[g] \colon A \to B より \text{dom}(f) = \text{dom}(g) かつ \text{cod}(f) = \text{cod}(g) が成り立つ。また F(f) = (\tilde{F} \circ \pi)(f) = \tilde{F}([f]) = \tilde{F}([g]) = (\tilde{F} \circ \pi)(g) = F(g) が成り立つので f \sim_{F} g つまり [f] = [g] が成り立つ。よって \tilde{F} は faithful functor である。

\square

4.4 Finitely presented categories

smallest congruence

書籍において \sim_{\Sigma} を g = g' \in \Sigma なら g \sim g' を満たす congruence の中で最小の congruence として定義しています。congruence の intersection が congruence になることから、 \sim_{\Sigma} が存在すると書かれていますが本当でしょうか？
これは、 g = g' \in \Sigma なら g \sim g' を満たす congruence が少なくとも一つは存在することを示さないと定義として意味がありません。ここでは以下の記事の内容を元に具体的に \sim_{\Sigma} を構成します。
www.orecoli.com

まず二項関係 \Sigma' を \Sigma' = \left\{ (b \circ f \circ a, b \circ g \circ a) \,\middle| \, (f,g) \in \Sigma,\, \forall a,b,\, \text{cod}(a) = \text{dom}(f),\, \text{dom}(b) = \text{cod}(f) \right\} で定義します。上の記事を参考に \Sigma' から生成される equivalence relation として \sim_{\Sigma} を定義します。このとき \sim_{\Sigma} が (f,g) \in \Sigma なら f \sim g を満たす最小の congruence であることを証明します。初めに \sim_{\Sigma} が congruence であることを証明します。

Lemma
\sim_{\Sigma} \text{ is a congruence}.

Proof.
任意の f,g \in {\bf{C}}_{1} に対して f \sim_{\Sigma} g であるとする。

  • n = 1 のとき

f = g であるとすると、 \text{dom}(f) = \text{dom}(g) かつ \text{cod}(f) = \text{cod}(g) は明らか。また任意の a,b に対して b \circ f \circ a = b \circ g \circ a であるから、 \sim_{\Sigma} が equivalence relation であることより b \circ f \circ a \sim_{\Sigma} b \circ g \circ a が成り立つ。
(f, g) \in \Sigma' とすると、 \exists (f',g') \in \Sigma と \exists x,y が存在して (f,g) = (y \circ f' \circ x, y \circ g' \circ x) と表される。このとき \text{dom}(f) = \text{dom}(g) かつ \text{cod}(f) = \text{cod}(g) は明らかである。また任意の a,b に対して (b \circ y \circ f' \circ x \circ a, b \circ y \circ g' \circ x \circ a) \in \Sigma' であるから、 b \circ f \circ a \sim_{\Sigma} b \circ g \circ a が成り立つ。
(g,f) \in \Sigma' の場合も (f,g) \in \Sigma' の場合と同様である。

  • n \gt 1 のとき

帰納法の仮定により \text{dom}(f) = \text{dom}(x_{n-1})、 \text{cod}(f) = \text{cod}(x_{n-1}) かつ 任意の a,b に対して b \circ f \circ a \sim_{\Sigma} b \circ x_{n-1} \circ a が成り立つ。一方で x_{n-1} = g、 (x_{n-1}, g) \in \Sigma'、 (g, x_{n-1}) \in \Sigma' のそれぞれの場合に対して、 n = 1 の場合と同様の議論により、 \text{dom}(x_{n-1}) = \text{dom}(g)、 \text{cod}(x_{n-1}) = \text{cod}(g) かつ 任意の a,b に対して b \circ x_{n-1} \circ a \sim_{\Sigma} b \circ g \circ a が成り立つ。
よって \sim_{\Sigma} が equivalence relation であることより \text{dom}(f) = \text{dom}(g)、 \text{cod}(f) = \text{cod}(g) かつ 任意の a,b に対して b \circ f \circ a \sim_{\Sigma} b \circ g \circ a が成り立つ。

\square

次に \sim_{\Sigma} が (f,g) \in \Sigma ならば f \sim g を満たす最小の congruence であることを証明します。 \sim_{\Sigma} が (f,g) \in \Sigma ならば f \sim_{\Sigma} g をみたすことは、 a = 1_{\text{dom}(f)}、 b = 1_{\text{cod}(f)} とすれば (f,g) \in \Sigma' となることから明らかです。

Lemma
\sim_{\Sigma} \text{ is the smallest congruence}.

Proof.
\sim を (f,g) \in \Sigma ならば f \sim g を満たす任意の congruence であるとする。
任意の f,g \in {\bf{C}}_{1} に対して f \sim_{\Sigma} g であるとする。

  • n = 1 のとき

f = g とすると、 \sim は equivalence relation であるから f \sim g が成り立つ。
(f,g) \in \Sigma' とすると、 \exists (f',g') \in \Sigma と \exists x,y が存在して (f,g) = (y \circ f' \circ x, y \circ g' \circ x) と表される。仮定より f' \sim g' が成り立ち、 \sim が congruence であることより f \sim g が成り立つ。
(g,f) \in \Sigma' の場合も (f,g) \in \Sigma' の場合と同様である。

  • n \gt 1 のとき

帰納法の仮定より f \sim x_{n-1} が成り立つ。一方で x_{n-1} = g、 (x_{n-1}, g) \in \Sigma'、 (g, x_{n-1}) \in \Sigma' のそれぞれの場合に対して、 n = 1 の場合と同様の議論により、 x_{n-1} \sim g が成り立つ。よって \sim の transitivity により f \sim g が成り立つ。

\square

参考書籍

Category Theory (Oxford Logic Guides)

Category Theory (Oxford Logic Guides)

  • 作者:Awodey, Steve
  • 発売日: 2008/01/10
  • メディア: ペーパーバック
圏論 原著第2版

圏論 原著第2版

二項関係から生成される同値関係に関する形式的な証明

数学

はじめに

数学の勉強をしていると、関係 \sim を次の等式を含むような最小の同値関係とする、という定義がよく出てきます。
しかし、この定義は関係 \sim の具体的な構成を与えていないので、この同値関係に関する証明をしようとすると途端に行き詰まってしまいます(例えば、商空間を定義域とするような関数が well-defined であることを証明する場合など)。
この記事では、二項関係から生成される同値関係を構成的に定義し、それが本当に最小の同値関係になっていることを証明します。
また同値類を定義し、同値類と同値関係に関して成り立つ基本的な事柄に関して補足します。

二項関係から生成される関係

R を任意の集合 X 上の二項関係であるとします。このとき、新しい X 上の二項関係 R' を次のように定義します。

\begin{align*}
\forall x,y \in X,\, (x,y) \in R' \iff &\exists n,\, \exists x_{0}, \dots , x_{n} \in X, \\
&x = x_{0} \\
&\land y = x_{n} \\
&\land \left( \forall 0 \leq i \leq n - 1,\, x_{i} = x_{i+1} \lor (x_{i}, x_{i+1}) \in R \lor (x_{i+1}, x_{i}) \in R \right)
\end{align*}

この R' が R を含むような最小の同値関係であることを示します。

Lemma
R \subseteq R'

Proof.
任意の x,y \in X に対して、 (x,y) \in R とすると、 n = 1、 x = x_{0}、 y = x_{1} とすると、 (x_{0}, x_{1}) \in R が成り立つので、 (x,y) \in R' が成り立つ。

\square

Lemma
R' \text{ is an equivalence relation}.

Proof.

  • reflexive

任意の x \in X に対して、 n = 1、 x = x_{0}、 x = x_{1} とすれば、 x_{0} = x_{1} が成り立つので、 (x,x) \in R' が成り立つ。

  • symmetric

任意の x,y \in X に対して、 (x,y) \in R' とすると、 \exists n,\ \exists x_{0}, \dots , x_{n} が存在して、 x = x_{0}、 y = x_{n}、 \forall 0 \leq i \leq n-1,\, x_{i} = x_{i+1} \lor (x_{i}, x_{i+1}) \in R \lor (x_{i+1},x_{i}) \in R を満たす。このとき、 x_{0}, \dots , x_{n} の順序を逆にした列 x_{n}, \dots, x_{0} を新たに x'_{0}, \dots x'_{n} とすると、これは y = x'_{0}、 x = x'_{n}、 \forall 0 \leq i \leq n-1,\, x'_{i} = x'_{i+1} \lor (x'_{i}, x'_{i+1}) \in R \lor (x'_{i+1},x'_{i}) \in R を満たす。よって (y,x) \in R' が成り立つ。

  • transitive

任意の x,y,z \in X に対して、 (x,y) \in R'、 (y,z) \in R' とすると、 \exists n,\, \exists x_{0}, \dots ,x_{n} と \exists n',\, \exists x'_{0}, \dots, x'_{n'} が存在して条件を満たす。このとき、列 x_{0}, \dots, x_{n}, x'_{0}, \dots, x'_{n'} を新たに列 x''_{0}, \dots , x''_{n + n' + 1} とすると、これは x = x''_{0}、 z = x''_{n+n'+1}、 \forall 0 \leq i \leq n + n',\, x''_{i} = x''_{i+1} \lor (x''_{i}, x''_{i+1}) \in R \lor (x''_{i+1}, x''_{i}) \in R を満たす。よって (x,z) \in R' が成り立つ。

\square

以上より、 R' が R を含む同値関係であることがわかりました。次に R' が R を含むような同値関係の中で最小であることを示します。

Lemma
R' \text{ is the least equivalence relation containing } R.

Proof.
任意の R'' を R を含む同値関係であるとする。任意の x,y \in X に対して、 (x,y) \in R' とすると \exists n,\, \exists x_{0}, \dots, x_{n} が存在して条件を満たす。このとき、 n に関する帰納法により証明する。

  • n = 1 のとき

x_{0} = x_{1} のときは R'' が同値関係であることより (x,y) \in R'' である。 (x_{0},x_{1}) \in R \lor (x_{1}, x_{0}) \in R のときは、 R'' が R を含むことより (x,y) \in R'' が成り立つ。

  • n \gt 1 のとき

帰納法の仮定より (x_{0}, x_{n-1}) \in R'' が成り立つ。 n = 1 のときと同様の議論により、 (x_{n-1}, x_{n}) \in R'' が成り立つ。よって R'' の transitivity により、 (x,y) \in R'' が成り立つ。

\square

同値類

集合 X 上の任意の同値関係 \sim が与えられているときに、任意の x \in X に対して次にように定義される集合を x の同値類と呼びます。
\begin{equation}
[x] = \left\{ y \in X \ \middle| \ x \sim y \right\}
\end{equation}
このとき、次の事柄が成り立ちます。

Lemma
\forall x,x',y \in X,\, y \in [x \land y \in [x'] \Rightarrow [x] = [x'] ]

Proof.
y \in [x]、 y \in [x'] より x \sim y、 x' \sim y が成り立つ。すると \sim が同値関係であることから、 x \sim x' が成り立つ。
すると任意の z \in X に対して、 z \in [x] \iff x \sim z \iff x' \sim z \iff z \in [x'] が成り立つ。よって [x] = [x'] である。

\square

これは集合 X が互いに素な同値類に分解されることを示しています。

同値類と同値関係の性質

最後に基本的な事柄を確認して終わりにします。これによって、同値関係にない要素は違う同値類に属することがわかります。

Lemma
\forall x,y \in X,\, [x = [y] \iff x \sim y ]

Proof.

  • only if case

y \in [y] であるから仮定より y \in [x] が成り立つ。すると定義より x \sim y が成り立つ。

  • if case

任意の z \in X に対して、仮定と \sim が同値関係であることより、 z \in [x] \iff x \sim z \iff y \sim z \iff z \in [y] が成り立つ。よって [x] = [y] である。

\square

Steve Awodey の Category Theory を読む : Chapter 3

数学 数学-圏論

Steve Awodey の Category Theory を読む シリーズトップ

3.2 Coproducts

Example 3.5

Lemma
M(A) + M(B) \cong M(A + B)

Proof.
i_{M(A)} \colon M(A) \to M(A + B) を M(A) の UMP より \left| i_{M(A)} \right| \circ \eta_{A} = \eta_{A+B} \circ i_{A} を満たすただ一つの arrow とする。同様に i_{M(B)} \colon M(B) \to M(A+B) を定める。このとき、 (M(A+B),i_{M(A)},i_{M(B)}) が M(A)、 M(B) の coproduct となることを示す。
任意の N \in \bf{Mon}_{0} と任意の f \colon M(A) \to N, g \colon M(B) \to N に対して、 \left| f \right| \circ \eta_{A} \colon A \to \left| N \right| と \left| g \right| \circ \eta_{B} \colon B \to \left| N \right| を考えると、 A + B の UMP より \exists !\, [\left| f \right| \circ \eta_{A}, \left| g \right| \circ \eta_{B}] \colon A + B \to \left| N \right| が存在する。すると M(A+B) の UMP より \exists !\, [f,g] \colon M(A+B) \to N が存在して、 \left| [f,g] \right| \circ \eta_{A+B} = [\left| f \right| \circ \eta_{A}, \left| g \right| \circ \eta_{B}] を満たす。この [ f,g ] に対して、

\begin{align*}
\left| [f,g] \circ i_{M(A)} \right| \circ \eta_{A} &= \left| [f,g] \right| \circ \left| i_{M(A)} \right| \circ \eta_{A} \\
&= \left| [f,g] \right| \circ \eta_{A+B} \circ i_{A} \\
&= [\left| f \right| \circ \eta_{A}, \left| g \right| \circ \eta_{B}] \circ i_{A} \\
&= \left| f \right| \circ \eta_{A}
\end{align*}

が成り立つので、 M(A) の UMP より [f,g] \circ i_{M(A)} = f が成り立つ。同様に [f,g] \circ i_{M(B)} = g が成り立つので、 [f,g] は diagram を可換にする。
次に、任意の h \colon M(A+B) \to N が diagram を可換にするとする。すると

\begin{align*}
\left| h \right| \circ \eta_{A+B} \circ i_{A} &= \left| h \right| \circ \left| i_{M(A)} \right| \circ \eta_{A} \\
&= \left| h \circ i_{M(A)} \right| \circ \eta_{A} \\
&= \left| f \right| \circ \eta_{A}
\end{align*}

が成り立つ。同様に \left| h \right| \circ \eta_{A+B} \circ i_{B} = \left| g \right| \circ \eta_{B} が成り立つので、 A+B の UMP より、 \left| h \right| \circ \eta_{A+B} = [\left| f \right| \circ \eta_{A}, \left| g \right| \circ \eta_{B}] である。よって M(A+B) の UMP より [f,g] = h が成り立つので、 M(A+B) は M(A)、 M(B) の coproduct である。

\square

free monoid の UMP や、coproduct の UMP を適宜使用する必要があってちゃんと証明しようとすると複雑ですね。coproduct の UMP を証明するために、diagram を可換にする arrow が存在することと、それがただ一つに決まることの2つを証明していることを確認してください。

Example 3.6

一般に (X, \mathcal{O}(X) )、 (Y, \mathcal{O}(Y) ) が位相空間のとき、 X + Y の位相は \mathcal{O}(X + Y) = \left\{ O_{X} + O_{Y} \,\middle| \, O_{X} \in \mathcal{O}(X),\, O_{Y} \in \mathcal{O}(Y) \right\} で定義されます。

Lemma
(X + Y, \mathcal{O}(X + Y) ) \text{ is a coproduct of } (X, \mathcal{O}(X) ) \text{ and } (Y, \mathcal{O}(Y) ).

Proof.
任意の (Z, \mathcal{O}(X) ) と任意の f \colon X \to Z, g \colon Y \to Z に対して、 [ f,g] \colon X + Y \to Z を Example 3.4 と同様に定義すると、可換性と唯一性は Example 3.4 で証明済みなので [ f,g] が continuous であることを示せばよい。
任意の O \in \mathcal{O}(Z) に対して、 {[f,g ]}^{-1}(O) = f^{-1}(O) + g^{-1}(O) であるが、 f、 g が continuous であることより、 f^{-1}(O) \in \mathcal{O}(X)、 g^{-1}(O) \in \mathcal{O}(Y) が成り立つ。 \mathcal{O}(X + Y) の定義より {[f,g ]}^{-1}(O) \in \mathcal{O}(X + Y) となるから、 [ f,g ] は continuous である。

\square

Example 3.9

この Example の証明は非形式的な証明でさらっと流されていますが、形式的に証明しようとすると結構大変です。
書籍では、binary relation \sim は4つの等式を含んだ最小の equivalence relation であるとだけ書かれていますが、具体的にどのように構成するのか書かれていません。4つの等式を M(\left| A \right| + \left| B \right|) 上の二項関係と表現したときに生成される最小の equivalence relation の構成については下の記事に書いたのでそちらを参照してください。
www.orecoli.com

i_{A}、 i_{B} が homomorphism となることは明らかなので省略します。 i_{A}(u_{A}) = [u_{A}] と i_{B}(u_{B}) = [u_{B}] が A + B において一致して、かつ A + B の単位元になる必要があるので、4つの等式の上の二つを含む equivalence relation で割る必要があるということを確認してください。
ここでは、書籍にあるように [f,g]([x \dots y]) = [f,g]'((x \dots y) ) で定義される [f,g] が well-defined であることを証明します。

Lemma
\begin{equation}
\forall [v], [w] \in M(\left| A \right| + \left| B \right|)\, / \sim,\, [v] = [w] \Rightarrow [f,g]([v]) = [f,g]([w])
\end{equation}

Proof.
4つの等式を表現する M(\left| A \right| + \left| B \right|) 上の二項関係を R とする。
先に参照した記事の内容より、 [v] = [w] \iff v \sim w が成り立つ。よって \exists n,\, \exists x_{0}, \dots ,x_{n} が存在して、 x_{0} = v、 x_{n} = w かつ \forall 0 \leq i \leq n-1,\, x_{i} = x_{i+1} \lor (x_{i},x_{i+1}) \in R \lor (x_{i+1},x_{i}) \in R が成り立つ。 n に関する帰納法により示す。

  • n = 1 のとき

v = w の場合は明らか。 (v,w) \in R のとき、 s, s' を \left| A \right| + \left| B \right| 上の任意の word とすると、 v = su_{A}s',\, w = ss' の場合を考える。このとき、

\begin{align*}
[f,g]'(su_{A}s') &= [f,g]'(s) \cdot f(u_{A}) \cdot [f,g]'(s') \\
&= [f,g]'(s) \cdot u_{M} \cdot [f,g]'(s') \\
&= [f,g]'(s) \cdot [f,g]'(s') \\
&= [f,g]'(ss')
\end{align*}

が成り立つので、 [f,g]([v]) = [f,g]([w]) が成り立つ。 v = su_{B}s',\, w = ss' の場合も同様である。
v = saa's',\, w = s(a \cdot_{A} a')s' のとき、

\begin{align*}
[f,g]'(saa's') &= [f,g]'(s) \cdot f(a) \cdot f(a') \cdot [f,g]'(s') \\
&= [f,g]'(s) \cdot f(a \cdot_{A} a') \cdot [f,g]'(s') \\
&= [f,g]'(s) \cdot [f,g]'(a \cdot_{A} a') \cdot [f,g]'(s') \\
&= [f,g]'(s(a \cdot_{A} a')s')
\end{align*}

が成り立つので、 [f,g]([v]) = [f,g]([w]) が成り立つ。 v = sbb's',\, w = s(b \cdot_{B} b')s' の場合も同様である。
(w,v) \in R の場合も同様に成り立つ。

  • n \gt 1 のとき

帰納法の仮定より、 [f,g]([x_{0}]) = [f,g]([x_{n-1}]) が成り立つ。また n = 1 の場合と同様の議論により、 [f,g]([x_{n-1}]) = [f,g]([x_{n}]) が成り立つ。よって [f,g]([v]) = [f,g]([w]) が成り立つ。

\square

[f,g] が homomorphism であることは [f,g]' が homomorphism であることから明らかです。
また \pi \colon M(\left| A \right| + \left| B \right|) \to M(\left| A \right| + \left| B \right|)\, / \sim を自然な homomorphism とすると、 [f,g] \circ \pi = [f,g]' が成り立ちます。任意の h \colon M(\left| A \right| + \left| B \right|)\, / \sim \to M が h \circ \pi = [f,g]' を満たすなら h = [f,g] が成り立つことも簡単に確かめられます。
最後に [f,g] が [f,g] \circ i_{A} = f、 [f,g] \circ i_{B} = g を満たすただ一つの arrow であることを証明します。

Lemma
\begin{equation}
\forall h \colon M(\left| A \right| + \left| B \right|)\, / \sim \to M,\, h \circ i_{A} = f \land h \circ i_{B} = g \Rightarrow h = [f,g]
\end{equation}

Proof.
h \circ \pi = [f,g]' を示せばよい。それには M(\left| A \right| + \left| B \right|) の UMP より、 \left| h \circ \pi \right| \circ \eta_{\left| A \right| + \left| B \right|} = \left[ \left| f \right|, \left| g \right| \right] を示せばよい。それには \left| A \right| + \left| B \right| の UMP より、 \left| h \circ \pi \right| \circ \eta_{\left| A \right| + \left| B \right|} \circ i_{\left| A \right|} = \left| f \right| かつ \left| h \circ \pi \right| \circ \eta_{\left| A \right| + \left| B \right|} \circ i_{\left| B \right|} = \left| g\right| を示せばよい。
任意の a \in A に対して、

\begin{align*}
(\left| h \circ \pi \right| \circ \eta_{\left| A \right| + \left| B \right|} \circ i_{\left| A \right|})(a) &= h([a]) \\
&= \left| h \circ i_{A} \right| (a) \\
&= \left| f \right| (a)
\end{align*}

が成り立つ。同様に、 \left| h \circ \pi \right| \circ \eta_{\left| A \right| + \left| B \right|} \circ i_{\left| B \right|} = \left| g\right| が成り立つので h = [f,g] が成り立つ。

\square

Example 3.10

Lemma
A + B \text{ is a coproduct of } A \text{ and } B.

Proof.
任意の X と任意の f \colon A \to X, g \colon B \to X に対して、 [f,g] \colon A + B \to X を [f,g](a,b) = f(a) + g(b) で定義する。すると ([f,g] \circ i_{A})(a) = [f,g](a,0) = f(a) が成り立つ。同様に [f,g] \circ i_{B} = g が成り立つので、 [f,g] は diagram を可換にする。
一方、任意の h \colon A + B \to X が diagram を可換にするとすると、任意の (a,b) \in A + B に対して、 h(a,b) = h((a,0) + (0,b) ) = (h \circ i_{A})(a) + (h \circ i_{B})(b) = f(a) + g(b) = [f,g](a,b) が成り立つ。よって A + B は A、 B の coproduct である。

\square

Proposition 3.11

証明の中で zero homomorphism という言葉が出てきます。 \bf{Ab} においては \{0\} は initial object かつ terminal object となり、そのような対象を zero object と呼びます。
この zero object を用いると、任意の対象 A,B 間に 0 \colon A \to \{0\} \to B なる arrow が存在することがわかります。( A \to \{0\} の箇所では \{0\} が terminal object であることを利用し、 \{0\} \to B の箇所では \{0\} が initial object であることを利用しています。)

3.4 Coequalizers

Example 3.20

集合圏 Sets において任意の f,g \colon A \rightrightarrows B に対して coequalizer を具体的に構成します。
R を R = \left\{ (f(a), g(a)) \, \middle| \, a \in A \right\} で定義される B 上の二項関係とし、 R' を R から生成される equivalence relation とします。このとき、 \pi \colon B \to B / R' を任意の b \in B に対して \pi(b) = [b] で定義します。

Lemma
\pi \circ f = \pi \circ g

Proof.
任意の a \in A に対して、 (\pi \circ f)(a) = [f(a)]、 (\pi \circ g)(a) = [g(a)] であるから、 [f(a)] = [g(a)] つまり (f(a),g(a)) \in R' を示せばよい。これは R' の定義より、 n = 1、 x_{0} = f(a)、 x_{1} = g(a) とすれば、 (f(a), g(a)) \in R であるから (f(a),g(a)) \in R' が成り立つ。

\square

次に任意の h \colon B \to C が h \circ f = h \circ g を満たすとき、 \overline{h} \colon B / R' \to C を \overline{h}([b]) = h(b) で定義します。このとき、 \overline{h} が well-defined であることを証明します。
f:id:hitotakuchan:20160406180220p:plain:w400

Lemma
\begin{equation}
\forall b,b' \in B,\, [b] = [b'] \Rightarrow \overline{h}([b]) = \overline{h}([b'])
\end{equation}

Proof.
[b] = [b'] であるから (b,b') \in R' である。よって \exists n,\, \exists x_{0}, \dots ,x_{n} が存在して、 x_{0} = b、 x_{n} = b' かつ \forall 0 \leq i \leq n-1,\, x_{i} = x_{i+1} \lor (x_{i},x_{i+1}) \in R \lor (x_{i+1},x_{i}) \in R が成り立つ。 n に関する帰納法により示す。

  • n = 1 のとき

b = b' なら \overline{h}([b]) = \overline{h}([b']) は明らかである。
(b,b') \in R なら \exists a \in A が存在して、 b = f(a) かつ b' = g(a) であるから、 \overline{h}([b]) = h(b) = h(f(a)) = h(g(a)) = h(b') = \overline{h}([b']) が成り立つ。
(b',b) \in R なら \exists a \in A が存在して、 b = g(a) かつ b' = f(a) であるから、 \overline{h}([b]) = h(b) = h(g(a)) = h(f(a)) = h(b') = \overline{h}([b']) が成り立つ。

  • n \gt 1 のとき

帰納法の仮定より \overline{h}([b]) = \overline{h}([x_{n-1}]) が成り立つ。 (x_{n-1}, b') に対して、 n = 1 の場合と同様の議論により \overline{h}([x_{n-1}]) = \overline{h}([b']) が成り立つ。よって \overline{h}([b]) = \overline{h}([b']) が成り立つ。

\square

\overline{h} \circ \pi = h が成り立つことは定義より明らかです。また \pi が epic であるから、 \overline{h} はただ一つに決まります。よって (B/R', \pi) は f,g の coequalizer になります。

参考書籍

Category Theory (Oxford Logic Guides)

Category Theory (Oxford Logic Guides)

  • 作者:Awodey, Steve
  • 発売日: 2008/01/10
  • メディア: ペーパーバック
圏論 原著第2版

圏論 原著第2版

Steve Awodey の Category Theory を読む : Chapter 2

数学 数学-圏論

Steve Awodey の Category Theory を読む シリーズトップ

2.1 Epis and monos

Example 2.4

poset category P において、任意の p,q \in P_{0} 間の arrow は p \leq q ならばただ一つ存在すると定義されました。

Lemma
\forall f \colon p \to q,\ f \text{ is both monic and epic.}

Proof.

  • f が monic であること。

任意の g,h \colon r \to p に対して、 f \circ g = f \circ h \Rightarrow g = h を示せば良いが、 r から p への arrow は定義よりただ一つに決まるので、 g = h が成り立つ。よって f は monic である。

  • f が epic であること。

任意の g, h \colon q \to s に対して、 g \circ f = h \circ f \Rightarrow g = h を示せば良いが、 q から s への arrow は定義よりただ一つに決まるので、 g = h が成り立つ。よって f は epic である。

\square

a function is epic iff surjective in Sets

Lemma
\forall A,B \in Sets_{0},\ \forall f \colon A \to B,\ f \text{ is epic} \Rightarrow f \text{ is surjective.}

Proof.
背理法により示す。 f が surjective ではないと仮定すると、 \exists b',\ \forall a \in A, \ f(a) \neq b' が成り立つ。一方、 A \neq \emptyset であるから、 \exists a' \in A が存在する。ここで function g \colon B \to B を次のように定義する。
\begin{equation}
g(b) = \begin{cases}
f(a') & b = b' \\
b & b \neq b' \\
\end{cases}
\end{equation}
明らかに g \neq 1_{B} が成り立つ。任意の a \in A に対して、 (g \circ f)(a) = g(f(a)) = f(a) = (1_{B} \circ f)(a) より g \circ f = 1_{B} \circ f が成り立つが、 f が epic であるから g = 1_{B} が成り立つ。これは g \neq 1_{B} と矛盾する。よって f は surjective である。

\square

Lemma
\forall A,B \in Sets_{0},\ \forall f \colon A \to B,\ f \text{ is surjective} \Rightarrow f \text{ is epic.}

Proof.
任意の C \in Sets_{0} と任意の g,h \colon B \to C に対して、 g \circ f = h \circ f \Rightarrow g = h を示せばよい。そのためには、任意の b \in B に対して、 g(b) = h(b) を示せばよい。 f が surjective であることより、 \exists a,\ f(a) = b が成り立つので、 g(b) = g(f(a)) = (g \circ f)(a) = (h \circ f)(a) = h(f(a)) = h(b) が成り立つ。よって f は epic である。

\square

any epi into a projective object splits

diagram を描ければいいのですが難しそうなので、証明を読む際は手元で diagram を書きながら読んでください。
以下の証明では、任意の圏 \bf{C} において P を projective object であるとします。

Lemma
\forall e \colon E \to P,\ e \text{ is epic} \Rightarrow e \text{ splits.}

Proof.
1_{P} と e に対して、 P が projective であることより、 \exists \bar{1_{P}} \colon P \to E が存在して e \circ \bar{1_{P}} = 1_{P} が成り立つ。よって e は split epi である。

\square

any retract of a projective object is projective

Lemma
\forall X' \in {\bf{C}}_{0},\ X' \text{is a restract of } P \Rightarrow X' \text{ is projective.}

Proof.
任意の epic e \colon E \to X と任意の f \colon X' \to X に対して、 \exists \bar{f} \colon X' \to E,\ e \circ \bar{f} = f を示す。 X' が P の rectact であることより、 \exists s \colon X' \to P,\ r \colon P \to X',\ r \circ s = 1_{X'} が成り立つ。一方、 P が projective であることより (f \circ r) \colon P \to X と e に対して、 \exists \overline{f \circ r} が存在して、 e \circ \overline{f \circ r} = f \circ r が成り立つ。 \bar{f} を \bar{f} = \overline{f \circ r} \circ s で定義すると、 e \circ \overline{f \circ r} \circ s = f \circ r \circ s = f \circ 1_{X'} = f が成り立つ。よって X' は projective である。

\square

2.3 Generalized elements

ultrafilter F に関する lemma

Lemma
F \text{ is an ultrafilter} \iff \forall b \in B,\ (b \in F \land \lnot b \notin F) \lor (b \notin F \land \lnot b \in F)

Proof.

  • only if case

任意の b に対して、 b \in F とする。 \lnot b \in F とすると、 F が filter であることより、 0 = b \land \lnot b \in F が成り立つ。よって F = B となるが、これは F が ultrafilter であることと矛盾する。
次に b \notin F とする。このとき、 \lnot b \in F であることを背理示す。
\lnot b \notin F であるとする。集合 F \cup \{b\} を考え、この集合から filter F' を構成する。このとき F \subsetneq F' が成り立つ。 \lnot b \in F' であるとすると、 \exists a \in F,\ a \land b \leq \lnot b が成り立つ。つまり、 a \land b = 0 が成り立つ。よって a \leq \lnot b が成り立つが、 F が filter であることより \lnot b \in F が成り立ち、これは \lnot b \notin F と矛盾する。よって \lnot b \notin F' が成り立ち、 F \subsetneq F' \subsetneq B が成り立つ。これは F が maximal であることと矛盾する。よって \lnot b \in F が成り立つ。

  • if case

F が仮定を満たすような filter であるとき、 \forall F',\ F' \text{ is a filter} \land F \subsetneq F' \Rightarrow F' = B を示す。
F \subsetneq F' より、 \exists b' \in F',\ b' \notin F が存在する。すると F の仮定より、 \lnot b' \in F が成り立つ。 F \subsetneq F' より \lnot b' \in F' であるから、 b' \in F' \land \lnot b' \in F' が成り立つ。 F' が filter であることより、 0 = b' \land \lnot b' \in F' である。よって F' = B となるので、 F は maximal filter である。

\square

Example 2.12

Lemma
\forall f,g \colon C \to D,\ f = g \iff \forall x \colon X \to C,\ f \circ x = g \circ x

Proof.

  • only if case

f = g より f \circ x = g \circ x は明らかに成り立つ。

  • if case

仮定が成り立つとすると、 x として 1_{C} を取ると f = f \circ 1_{C} = g \circ 1_{C} = g が成り立つ。

\square

2.5 Examples of products

3

\bf{Cat} において、任意の圏 \bf{C}, \bf{D} の product \bf{C} \times \bf{D} が存在することを示します。証明することがたくさんあるので一つずつ確認していきましょう。

\bf{C} \times \bf{D} が圏であること

Lemma
{\bf{C}} \times {\bf{D}} \text{ is a category.}

Proof.
({\bf{C}} \times {\bf{D}})_{0} = \left\{ (c,d)\ \middle| \ c \in {\bf{C}}_{0},\,d \in {\bf{D}}_{0} \right\}、 \text{Hom}_{\bf{C} \times \bf{D}}((c,d),(c',d') ) = \left\{ (f,g)\ \middle| \ f \in \text{Hom}_{\bf{C}}(c,c'),\, g \in \text{Hom}_{\bf{D}}(d,d') \right\}、 (f', g') \circ_{\bf{C} \times \bf{D}} (f,g) = (f' \circ_{\bf{C}} f, g' \circ_{\bf{D}} g)、 1_{(c,d)} = (1_{c}, 1_{d}) で {\bf{C}} \times {\bf{D}} を定義する。
すると圏 \bf{C}, \bf{D} の性質より、 \circ_{\bf{C} \times \bf{D}} と 1_{(c,d)} が associativity と unit low を満たすことは明らかである。よって \bf{C} \times \bf{D} は圏となる。

\square

\pi_{1}, \pi_{2} が functor であること

Lemma
\pi_{1} \colon {\bf{C} \times \bf{D}} \to {\bf{C}}, \pi_{2} \colon {\bf{C} \times \bf{D}} \to {\bf{D}} \text{ are functors.}

Proof.
\pi_{1} を 任意の (c,d) \in ({\bf{C} \times \bf{D}}_{0}) と任意の (f,g) \colon (c,d) \to (c',d') に対して、 \pi_{1_{0}}((c,d) ) = c、 \pi_{1_{1}}((f,g) ) = f で定義する。
すると、 \pi_{1_{1}}((f,g) \colon (c,d) \to (c',d') ) = f \colon c \to c' = f \colon \pi_{1_{0}}(c,d) \to \pi_{1_{0}}(c',d') が成り立つので、 \pi_{1} は functor の条件 (a) を満たす。
\pi_{1_{1}}(1_{(c,d)}) = \pi_{1_{1}}((1_{c},1_{d}) ) = 1_{c} = 1_{\pi_{1_{0}}((c,d) )} が成り立つので、 \pi_{1} は functor の条件 (b) を満たす。
任意の (f',g') \colon (c',d') \to (c'',d'') に対して、 \pi_{1_{1}}((f',g') \circ_{\bf{C} \times \bf{D}} (f,g) ) = \pi_{1_{1}}((f' \circ_{\bf{C}} f, g' \circ_{\bf{D}} g) ) = f' \circ_{\bf{C}} f = \pi_{1_{1}}((f',g') ) \circ_{\bf{C}} \pi_{1_{1}}((f, g) ) が成り立つので、 \pi_{1} は functor の条件 (c) を満たす。よって \pi_{1} は functor である。
\pi_{2} に関しても同様である。

\square

\bf{C} \times \bf{D} が product であること

Lemma
{\bf{C} \times \bf{D}} \text{ is a product of } {\bf{C}} \text{ and } {\bf{D}}.

Proof.
任意の \bf{X} と、任意の F \colon {\bf{X}} \to {\bf{C}},G \colon {\bf{X}} \to {\bf{D}} に対して、 \left< F,G \right> \colon {\bf{X}} \to {\bf{C} \times \bf{D}} を \left< F,G \right>_{0}(x) = (F_{0}(x), G_{0}(x) )、 \left< F,G \right>_{1}(f) = (F_{1}(f), G_{1}(f) ) で定義する。
すると、

\begin{align*}
\left< F,G \right>_{1}(f \colon x \to x') &= (F_{1}(f), G_{1}(f) ) \colon (F_{0}(x), G_{0}(x) ) \to (F_{0}(x'), G_{0}(x') ) \\
&= (F_{1}(f), G_{1}(f) ) \colon \left< F,G \right>_{0}(x) \to \left< F,G \right>_{0}(x')
\end{align*}

が成り立つので、 \left< F,G \right> は functor の条件 (a) を満たす。
\left< F,G \right>_{1}(1_{x}) = (F_{1}(1_{x}), G_{1}(1_{x}) ) = (1_{F_{0}(x)}, 1_{G_{0}(x)}) = 1_{\left< F,G \right>_{0}(x)} が成り立つので、 \left< F,G \right> は functor の条件 (b) を満たす。
任意の f \colon x \to x', f' \colon x' \to x'' に対して、

\begin{align*}
\left< F,G \right>_{1}(f' \circ_{\bf{X}} f) &= (F_{1}(f' \circ_{\bf{X}} f), G_{1}(f' \circ_{\bf{X}} f) ) \\
&= (F_{1}(f') \circ_{\bf{C}} F_{1}(f), G_{1}(f') \circ_{\bf{D}} G_{1}(f) ) \\
&= (F_{1}(f'), G_{1}(f') ) \circ_{\bf{C} \times \bf{D}} (F_{1}(f), G_{1}(f) ) \\
&= \left< F,G \right>_{1}(f') \circ_{\bf{C} \times \bf{D}} \left< F,G \right>_{1}(f)
\end{align*}

が成り立つので、 \left< F,G \right> は functor の条件 (c) を満たす。よって \left< F,G \right> は functor である。
このとき、 \pi_{1_{0}} \circ \left< F,G \right>_{0} = F_{0},\ \pi_{1_{1}} \circ \left< F,G \right>_{1} = F_{1} と \pi_{2_{0}} \circ \left< F,G \right>_{0} = G_{0},\ \pi_{2_{1}} \circ \left< F,G \right>_{1} = G_{1} が成り立つので、diagram は可換となる。
また、任意の H \colon X \to {\bf{C} \times \bf{D}} に対して、 H が diagram を可換とするなら、 H_{0}(x) = (F_{0}(x), G_{0}(x) )、 H_{1}(f) = (F_{1}(f), G_{1}(f) ) が成り立つ。よって、 H = \left< F,G \right> となり diagram を可換とする functor はただ一つに決まる。
以上より、 \bf{C} \times \bf{D} は \bf{C} と \bf{D} の product である。

\square

product of posets constructed in \bf{Cat}

\bf{Pos} の要素である poset それ自体を圏としてみた場合、poset 間の写像が functor であることと、monotone function であることは同一視できるのでした。よってここで確認するべきことは、先の product の定義が poset になるかどうかということです。
任意の poset P、 Q に対して、 P \times Q は (P \times Q)_{0} = \left\{ (p,q)\ \middle| \ p \in P,\, q \in Q \right\}、 \text{Hom}_{P \times Q}((p,q), (p',q') ) = \left\{ (f,g)\ \middle| \ f \in \text{Hom}_{P}(p,p'),\, q \in \text{Hom}_{Q}(q,q') \right\} で定義される。一方、Hom の定義は (p,p') \leq (q,q') \iff p \leq p' \land q \leq q' と同値です。
このように P \times Q に順序を入れた時に、 P \times Q が poset となることは P、 Q がそれぞれ poset であることより明らかです。
よって、 \bf{Cat} において構成した product が \bf{Pos} において product になることが確認できました。
\bf{Mon} の場合も同様です。

2.6 Categories with products

\times \colon \bf{C} \times \bf{C} \to \bf{C} is a functor

Lemma
\times \colon {\bf{C}} \times {\bf{C}} \to {\bf{C}} \text{ is a functor.}

Proof.
任意の product (A \times A', p_{1}, p_{2}),\,(B \times B', q_{1}, q_{2}) と 任意の f \colon A \to B, f' \colon A' \to B' に対して、 \times \colon \bf{C} \times \bf{C} \to \bf{C} を \times_{0}((A,A') ) = A \times A'、 \times_{1}((f, f') ) = f \times f' で定義する。
\times_{1}((f,f') \colon (A,A') \to (B,B') ) = f \times f' \colon A \times A' \to B \times B' = f \times f' \colon \times_{0}((A,A') ) \to \times_{0}((B,B') ) が成り立つので、 \times は functor の条件 (a) を満たす。
次に、 \times_{1}((1_{A},1_{A'}) ) = 1_{A} \times 1_{A'} であるが、これは定義より p_{1} \circ (1_{A} \times 1_{A'}) = 1_{A} \circ p_{1}、 p_{2} \circ (1_{A} \times 1_{A'}) = 1_{A'} \circ p_{2} を満たす。一方で 1_{A \times A'} も p_{1} \circ 1_{A \times A'} = 1_{A} \circ p_{1}、 p_{2} \circ 1_{A \times A'} = 1_{A'} \circ p_{2} を満たす。よって、 A \times A' の UMP より、 1_{A} \times 1_{A'} = 1_{A \times A'} が成り立つので、 \times は functor の条件 (b) を満たす。
最後に、任意の product (C \times C', r_{1}, r_{2}) と g \colon B \to C, g' \colon B' \to C' に対して、 \times_{1}((g,g') \circ (f,f') ) = \times_{1}((g \circ f, g' \circ f') ) = (g \circ f) \times (g' \circ f') である。これは、定義より r_{1} \circ ((g \circ f) \times (g' \circ f') ) = g \circ f \circ p_{1}、 r_{2} \circ ((g \circ f) \times (g' \circ f') ) = g' \circ f' \circ p_{2} を満たす。
一方で、 (g \times g') \circ (f \times f') に対して、

\begin{align*}
r_{1} \circ ((g \times g') \circ (f \times f') ) &= (r_{1} \circ (g \times g') ) \circ (f \times f') \\
&= (g \circ q_{1}) \circ (f \times f') \\
&= g \circ (q_{1} \circ (f \times f') ) \\
&= g \circ f \circ p_{1}
\end{align*}

が成り立ち、同様に r_{2} \circ ((g \times g') \circ (f \times f') ) = g' \circ f' \circ p_{2} が成り立つ。よって C \times C' の UMP より (g \circ f) \times (g' \circ f') = (g \times g') \circ (f \times f') = \times_{1}((g,g') ) \circ \times_{1}((f,f') ) が成り立つ。よって \times は functor の条件 (c) を満たす。

\square

product of I-indexed family of object (X_{i})_{i \in I}

\prod_{i \in I} X_{i} と (\pi_{i} \colon \prod_{i \in I} X_{i} \to X_{i})_{i \in I} の組み (\prod_{i \in I} X _{i}, (\pi_{i})_{i \in I}) が (X_{i})_{i \in I} の product であるとは、任意の Y と 任意の (f_{i} \colon Y \to X_{i})_{i \in I} に対して、ただ一つの f \colon Y \to \prod_{i \in I} X_{i} が存在して、任意の i \in I に対して、 \pi_{i} \circ f = f_{i} が成り立つこととして定義されます。

参考書籍

Category Theory (Oxford Logic Guides)

Category Theory (Oxford Logic Guides)

  • 作者:Awodey, Steve
  • 発売日: 2008/01/10
  • メディア: ペーパーバック
圏論 原著第2版

圏論 原著第2版