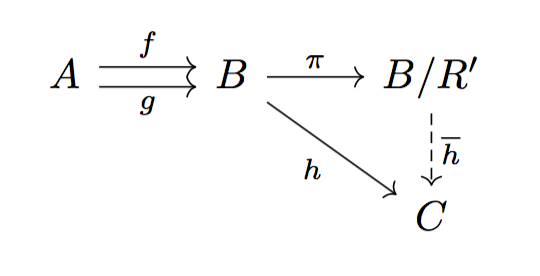Steve Awodey の Category Theory を読む シリーズトップ
5.2 Pullbacks
Proposition 5.5
only if case しか証明されていないので、if case の証明を補っておきます。
任意の に対して、
が成り立つとする。
が pullback であることより、
が存在して
かつ
を満たす。
このとき、 に対して、
であるから、
の UMP より
が成り立つ。
次に、任意の に対して、
が成り立つすると、
に対して
が成り立つ。よって pullback の UMP より
が成り立つ。
Exercise 3
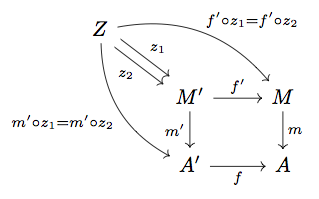
任意の に対して、
が成り立つとする。このとき、
が成り立つが、
が monic であることより
が成り立つ。
が pullback であることより、
が存在して、
かつ
を満たすが、
も diagram を可換にするので
が成り立つ。よって
は monic である。
5.3 Properties of pullbacks
Two pullbacks lemma
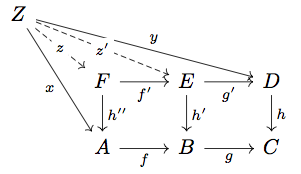
任意の と
に対して、
が成り立つとする。すると right square が pullback であることより、
が存在して
かつ
を満たす。さらに left square が pullback であることより
が存在して
かつ
を満たす。
次に、任意の に対して
かつ
が成り立つとする。
は
と
が成り立つから、right square の UMP より
が成り立つ。すると left square の UMP より
が成り立つ。
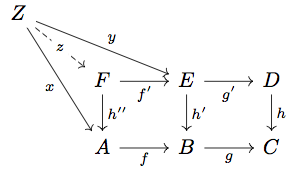
任意の と
に対して、
とする。
が成り立ち、outer rectangle が pullback であることより
が存在して
かつ
を満たす。
が成り立つことと、right square が pullback であることより
が成り立つ。
次に、任意の に対して
かつ
が成り立つとする。すると
が成り立つので、outer rectangle の UMP より
が成り立つ。
Proposition 5.10
証明自体は難しくないので詳細は省略します。一般に pullback は up to isomorphism でしか決まりません。よって、この functor の存在を言うためには選択公理を仮定するか、後で出てくる skeletal という概念を用いて圏
は skeletal であるという条件を付け加えないといけないと思います。
Example 5.13
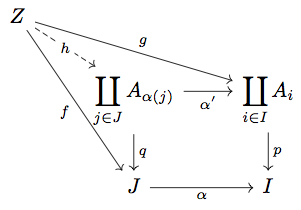
で定義する。
であるから
は well-defined である。
任意の と
に対して、
が成り立つとする。このとき、任意の
に対して
とするとき、
を
で定義する。これは
が成り立つので
となり well-defined である。また、
かつ
が成り立つので、
は diagram を可換にする。
次に、任意の が
かつ
を満たすとする。任意の
に対して
とすると、
より
が成り立つ。また
とすると、
より
が成り立つ。よって
が成り立つ。
5.4 Limits
Proposition 5.14
上の two-pullback lemma の場合もそうでしたが、証明が easy diagram chase とだけ書かれていて省略されている場合、私の経験上全然 easy じゃないことが多いので補足しておきます。
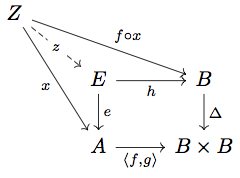
初めに が monic であることを示す。
任意の に対して、
が成り立つとする。すると
が成り立つ。よって
は monic である。
次に、 と
が成り立つので、
が成り立つ。
最後に、任意の に対して、
が成り立つとする。このとき
かつ
が成り立つから
の UMP より
が成り立つ。すると
が pullback であることより、
が存在して
かつ
を満たす。
Exercise 3 より が monic なら
は monic となるので
を満たす
はただ一つに決まる。よって
は
と
の equalizer である。
5.6 Colimits
Direct limits of groups
が
-colimits であることの証明は簡単ではないです。ここでは詳細は証明は省略しますが、以下の記事で R 加群の場合の direct limit に関する基本的な性質の証明を行っているので、詳しく証明を確認したい人は参照してください。
参考書籍

Category Theory (Oxford Logic Guides)
- 作者:Awodey, Steve
- 発売日: 2008/01/10
- メディア: ペーパーバック

- 作者:スティーブ アウディ
- 発売日: 2015/09/19
- メディア: 単行本